はじめに
こんにちは。 2022年9月2日から9月5日にかけて開催された ICFP Programming Contest 2022 にチームPigimarlとして参加しました。 メンバーは今西、江藤、柴田、杉森の4名です。 会場は用意せず、オンラインで各自が自由な時間に作業を行うという形で取り組みました。
結果は 世界3位 で、かなりの上位に食い込むことができました。 この記事では、コンテスト内で実装したソルバーやビジュアライザ・採点用のポータルサイトについて紹介します。
↓これは我がチームのお絵かきロボット君が懸命に目的の画像を再現した様子。
問題概要
今回の課題は「一定の命令セットを備えたお絵かきロボットを操作して、目的の画像にできるだけ近い画像を再現する」というものでした。 各命令の実行にはコストがかかり、コストを抑えつつ画像の再現度を高めることが求められます。
ロボットによるお絵かきは「キャンバスをタテ・ヨコに分割 or 統合すること」「分割された長方形の領域を一色で塗りつぶすこと」を繰り返して行います。 この操作とコストの設定が絶妙で、操作する対象の領域が狭いほどコストが高くなっています。 精密な再現をしようとするとコストが嵩んでしまうので、再現度とのトレードオフをしっかり考える必要があります。
ちなみに、ICFPC お馴染みの問題の仕様変更は今年も健在でしたが、その変更内容は控えめで問題の本質は終始変わらなかったように思います。 結果として仕様変更に振り回されることなく72時間腰を据えて問題に取り組むことができました。
ソルバー
ここからは、ソルバーの具体的なアルゴリズムについて説明していきます。 大きく分けて3つのポイントがあります。
原点塗り
1つ目のポイントは、画像の描画の方法です。
最初に試した方法は、キャンバス全体を粗いグリッドに分割し、各領域を一色で塗りつぶすというものでした。 この方法は、狭い領域を対象とした操作をキャンバス全体で繰り返すため、コストが非常に高くなってしまいます。
最終的に採用した方法は、原点 (左下) を含むような長方形を繰り返し描画していくというものです。 文章では伝わりづらいと思うので、実際に描画されている様子をご覧ください。
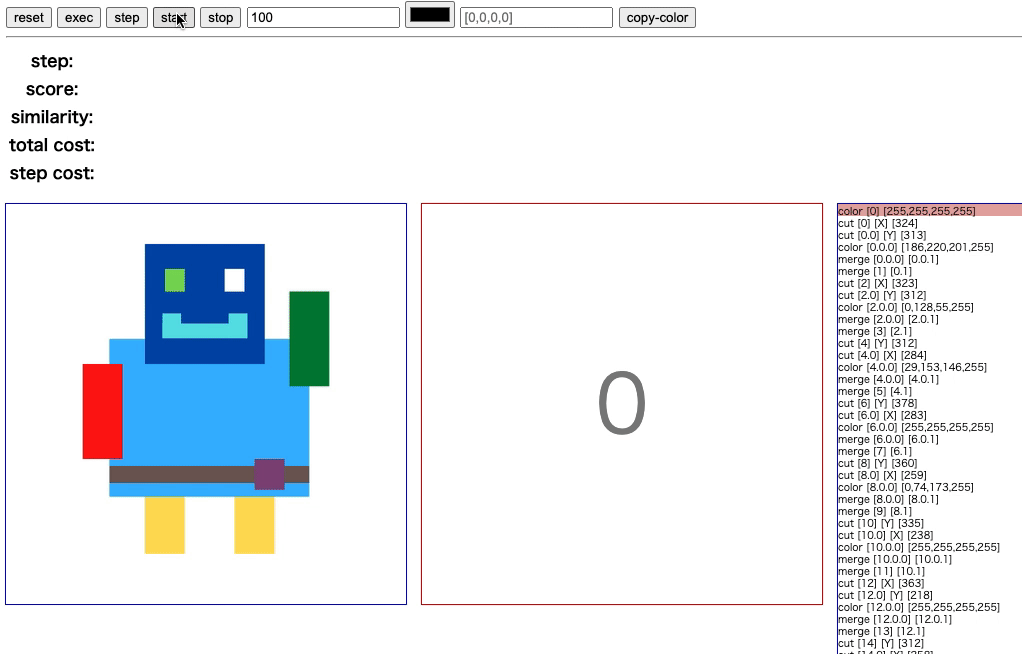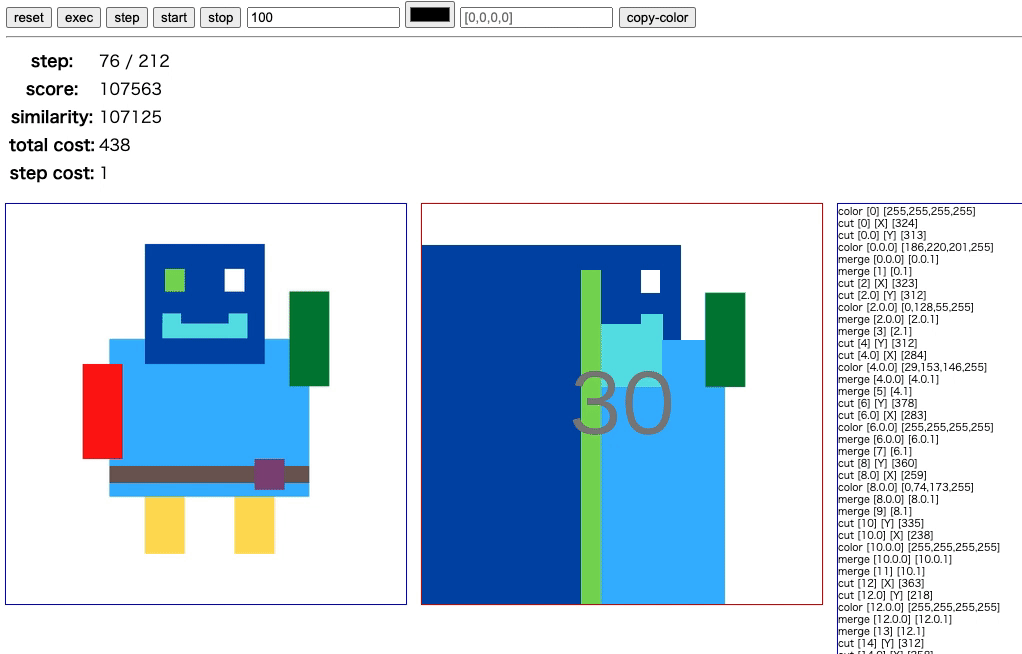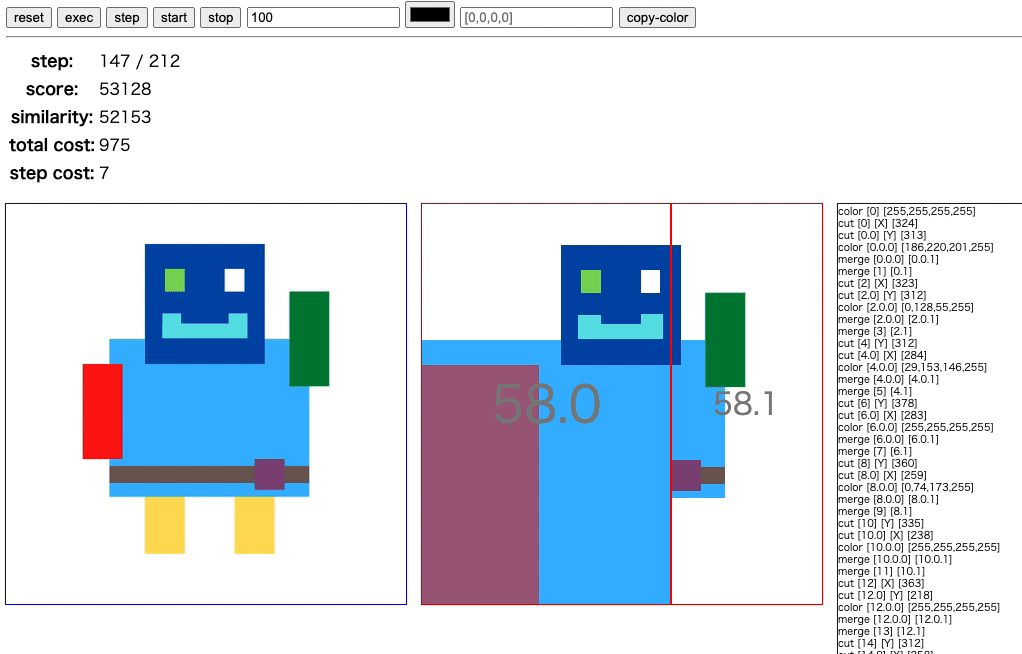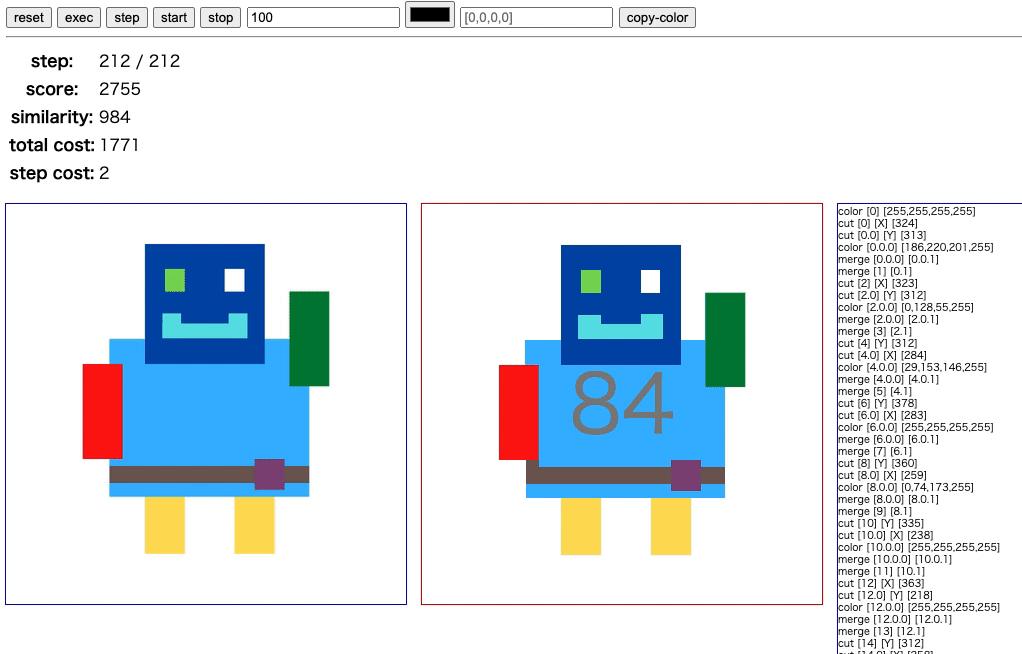
右上から左下へ長方形をどんどん上書きしながら描いています。 この方法ならば、操作対象の長方形はほとんどが大きいサイズなので、コストを抑えることができます。
色選び
2つ目のポイントは、各領域の色の選択方法です。
今回の課題の目標は「目的の画像にできるだけ近い画像を再現する」というものです。 目的の画像と生成した画像の間の乖離度の計算式は「各ピクセルのRGB空間上のユークリッド距離の総和」で定義されます。 これを踏まえ、各領域に単色を塗る際には乖離度をできるだけ小さくするようなRGB値の選択が求められます。
最初は深く考えず、領域内のピクセルの色の平均値を採用していました。 これは「各ピクセルの二乗誤差の総和」を最小化する場合には最適であるため、今回のケースでも良い近似値を与えると思っていました。
しかし、あるタイミングで平均値を中央値(RGBそれぞれで中央値を取ったもの)へ変更したところ、スコアが大きく改善しました。 例えば一次元に単純化して考えてみると、週3回東京へ、週2回大阪へ通勤する場合、東京・大阪間を 2:3 に内分する地点よりも、東京に住んだ方が移動距離の総和は小さくなります。 これと似たようなことがRGB空間においても成り立つようです。
一般に、n次元空間において各点までのユークリッド距離の総和を最小化するような点は Geometric median と呼ばれており、効率的な計算方法も知られているようです。 しかし、私たちのソルバーでは計算速度を優先し、中央値を代わりに使うことにしました。 スコアを見るかぎり、中央値は十分良い近似だったようです。
焼きなまし
3 つ目のポイントは、原点を含む長方形集合の配置と描画順の計算方法です。
他の上位チームはDP(動的計画法)を用いて計算しているところが多かったようですが、私たちのソルバーでは焼きなまし法を用いて計算を行いました。 状態として長方形の右上の座標の集合を管理し、近傍は
- 長方形の右上座標を上下左右に数ピクセル動かす
- 長方形を追加する
- 長方形を削除する
の3通りです。 これらの操作を行っても、キャンバスの一部しか差分が発生しないため、差分のみを計算することで計算量を抑えることができます。 高速化の結果、最終的には200,000回 / 分ほどのイテレーションを回せるようになりました。
他の上位チームのDP解法と比較した際のアピールポイントとしては、盤面の表現力が高いという点が挙げられます。 DP解法では、長方形を再帰的に分割していったような盤面のみを探索空間とするチームが多かったようです。 一方、この焼きなまし法では、長方形の右上の座標の集合を状態として持って探索を行うため、例えば2つの長方形が重なってL字型の領域が発生するような盤面も探索範囲とすることができます。
+α: 前処理
実はお絵かきロボットには他の命令もあり、同じ形の領域の内容をswapすることができます。 (図は 公式問題文 より)
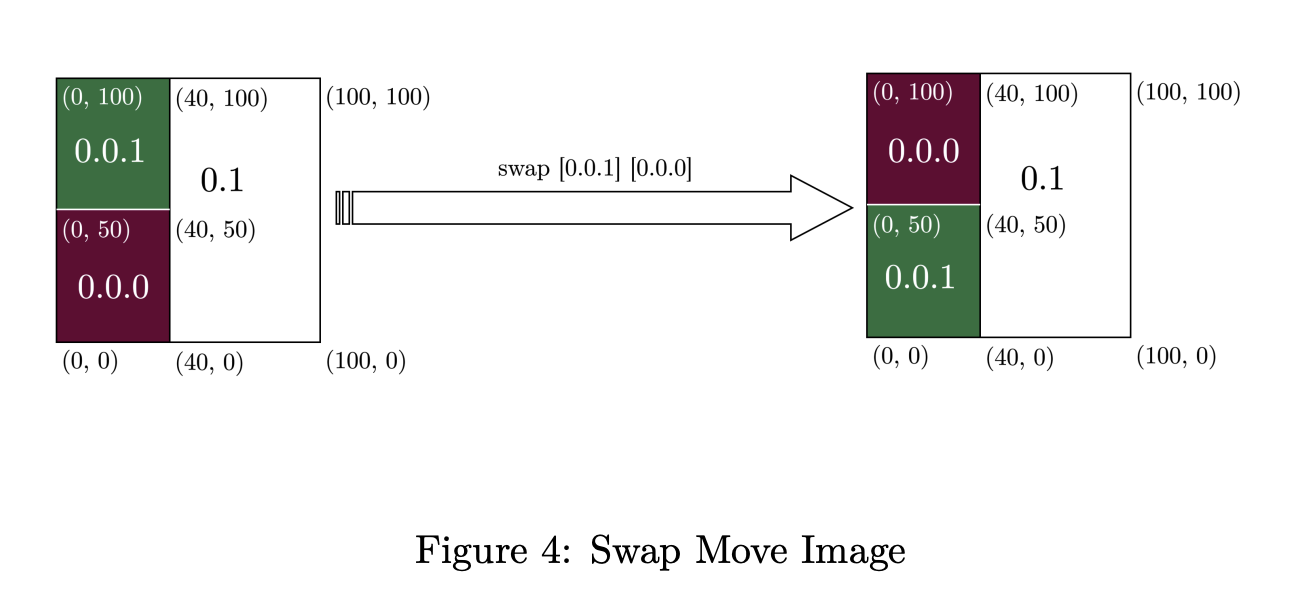
この操作も例によって領域が狭いほどコストが高くなってしまうので、あまり精密な再現のために使うことはできません。 使うとすればキャンバス全体を大きく切って大胆なswapをすることになるのですが、これを活用するため画像の前処理を行いました。
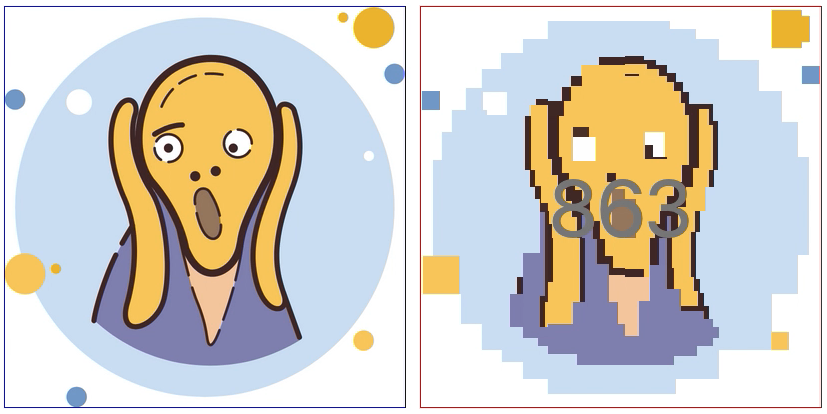
先に説明したソルバーの性質上、原点から遠い場所ほど低コストで精密な画像の再現ができます。 つまり目的の画像が原点付近でシンプルであればあるほど嬉しいのですが、ここで大きな領域のswapが使えます。
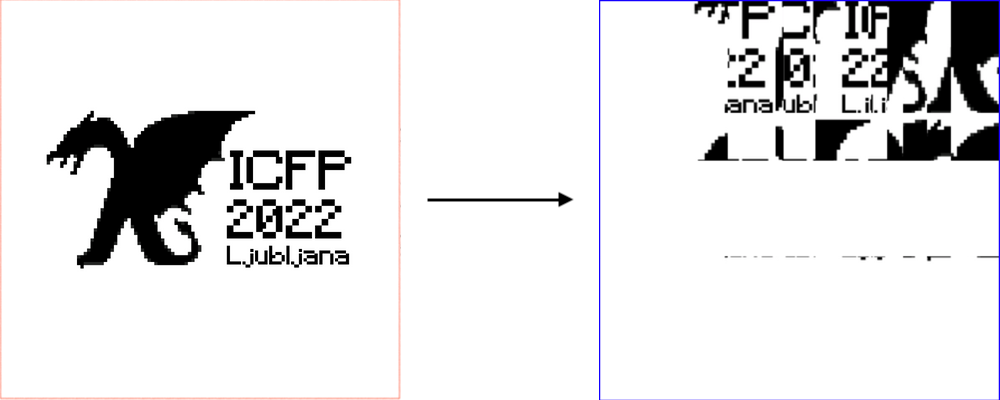
左がオリジナルの目的画像で、右が前処理後の目的画像です。 このように難所を隅に寄せるような前処理をswapを使って行い、前処理後の画像を先述のソルバーに与えます。 最後に、ソルバーの出力の末尾にちょうど前処理の逆となるような操作列を加えることで、元通りオリジナルの画像を再現することができます。
ビジュアライザー
今年も公式でビジュアライザーが提供されていました。 ただ、そちらは各ブロックの番号や枠線が表示されなかったりとソルバーを開発する上で欲しい機能が提供されていなかったため独自にビジュアライザーを作りました(この記事に貼られている画像は独自ビジュアライザーのものです)。
独自ビジュアライザーはプログラムを1行ずつ実行するステップ実行機能や一定時間毎にステップ実行をするアニメーション機能、目的画像の任意のピクセルの色を抽出するカラーピッカー機能などが提供されています。

採点インフラ
今年の問題は、複数のテストケースに対して、手元でできるだけ良い解を作成して提出するというICFPCによくある形式だったため、 2019年のICFPC で作成していた採点インフラを再利用することにしました。
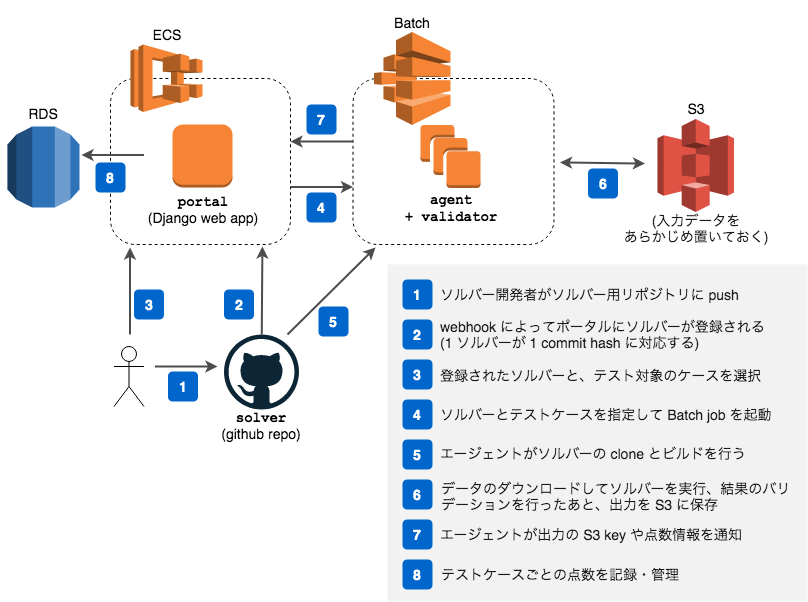
インフラ構成や採点実行までの流れは2019年のものと同じなので、詳細は当時のブログをご覧ください。 なお、コンテスト開始直後にインフラの構築を開始したのですが、全て手作業によるものだったために様々なところでハマり、採点が管理・実行できるようになるまでに無駄に時間がかかってしまいました。 今後も再利用する機会がありそうなので、インフラもコード化しておきたいところ…!
独自ポータルサイト
こちらも2019年に作成したDjango製のWebアプリにいくつか手を加える形で作成しました。
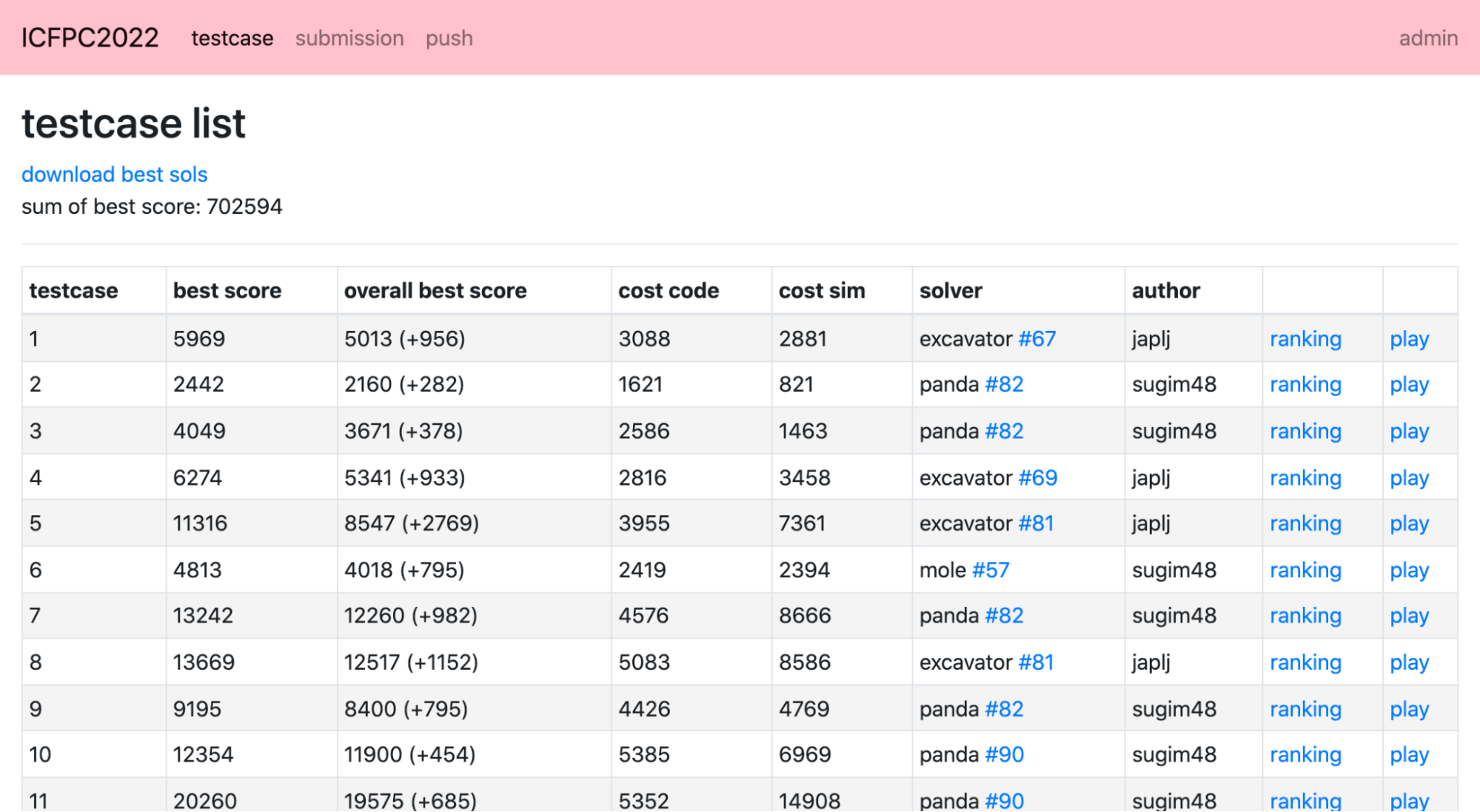
テストケースとそれに対応するチーム内の最適解の一覧。 全チーム横断のベストスコアとの差分も表示しています(コンテスト主催側で用意されていたベストスコア取得APIを利用しました)。 これのおかげで、コンテスト終盤にスコアを大きく改善できる点に気づくことができました。
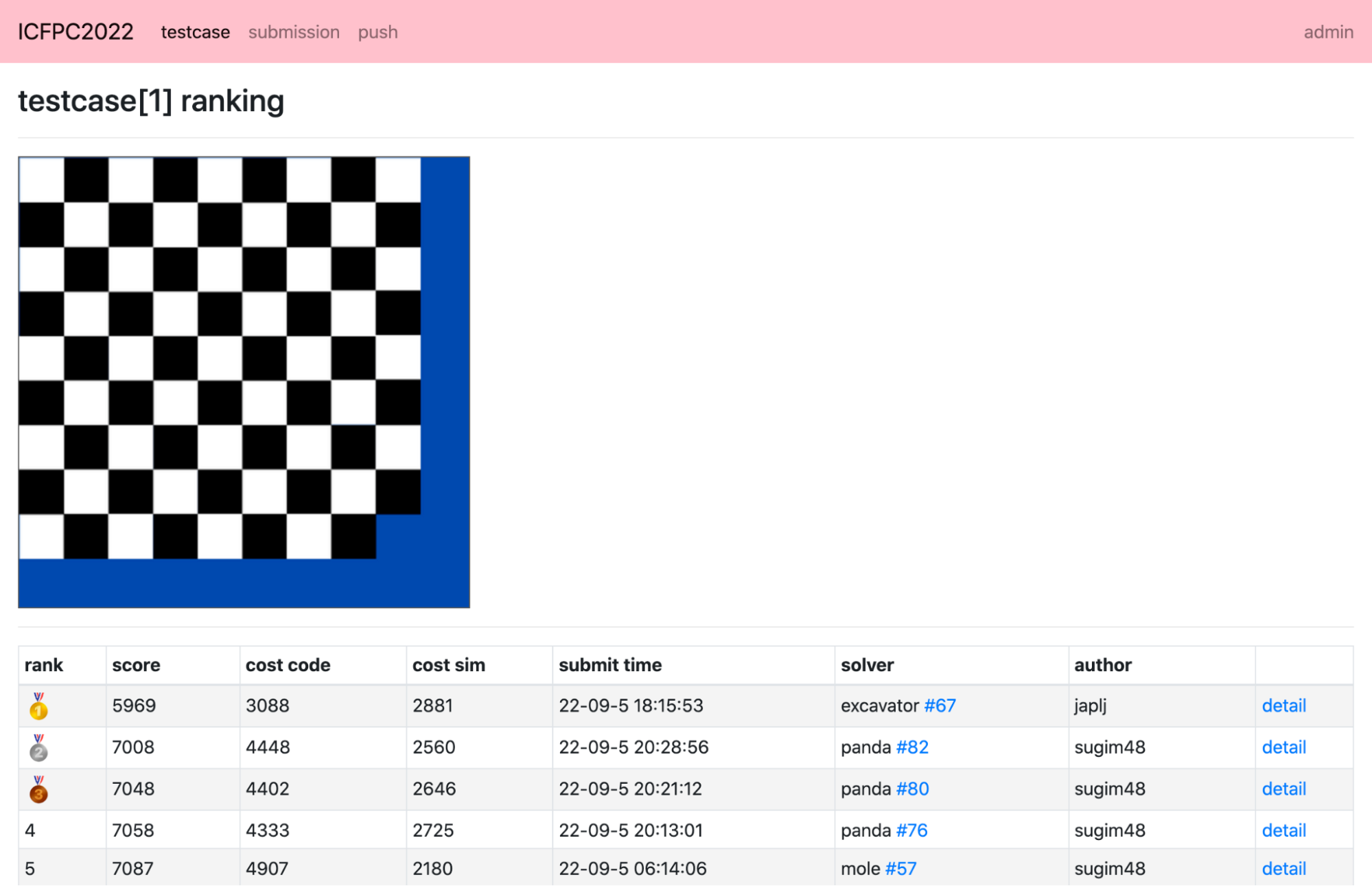
あるテストケースに対して実行されたソルバーの解のランキング。
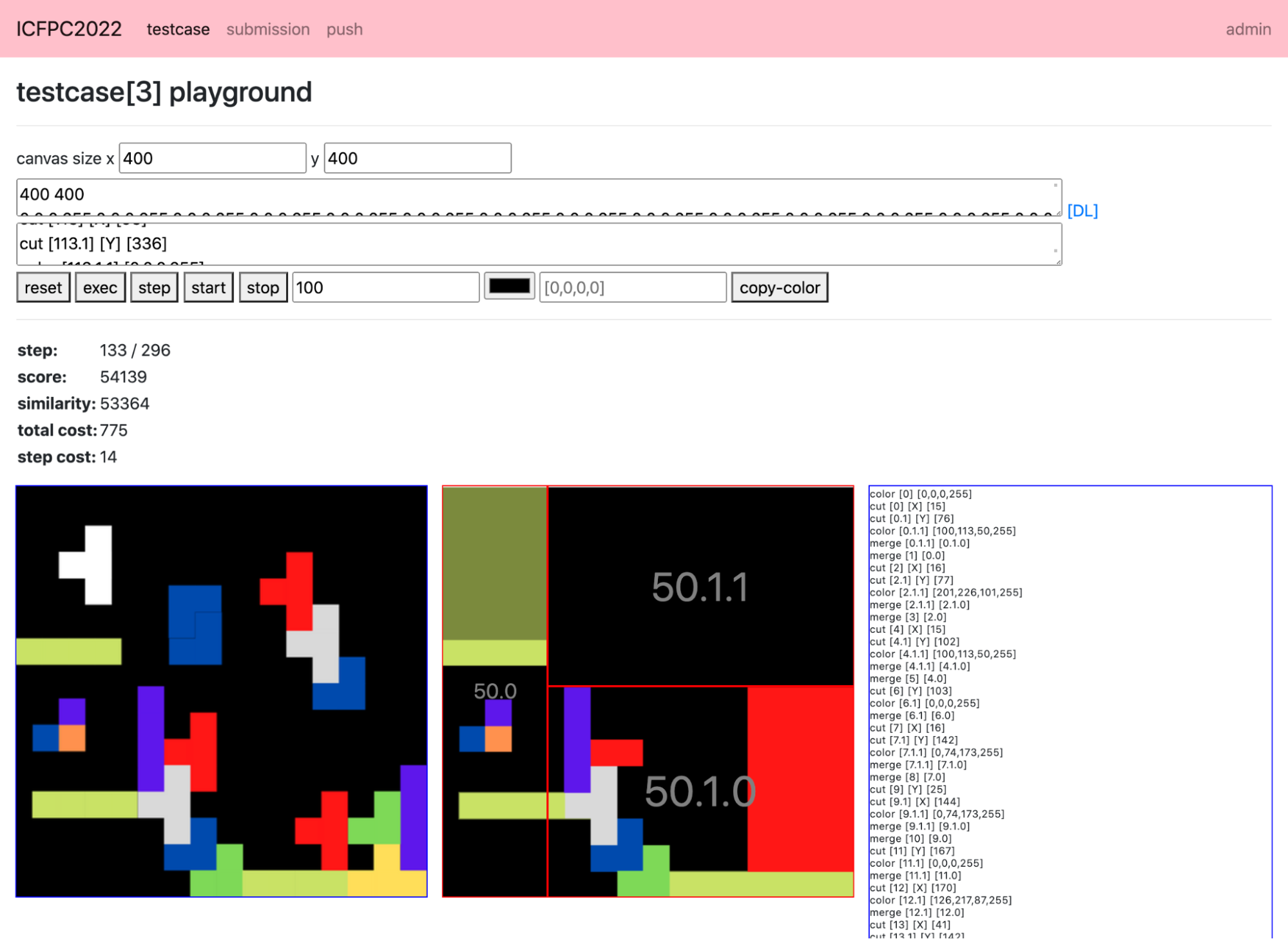
ポータルサイト上でビジュアライザも確認できます。 ちなみに、S3上の入出力データの取得にはPresigned URLを利用しています。
終わりに
今回のコンテストでは3位という好順位を取ることができましたが、1, 2位にはスコアで水を開けられてしまっています。 具体的な改善案をまだ残した状態でコンテスト時間終了を迎えたことは悔しくもあり、一方で同時により上位を現実的に目指せる伸びしろがあるとも感じました。
最後まで読んでいただきありがとうございました!

主にバックエンドの開発を担当
今西健介
リクルートグループ新卒入社5年目。ビートマニアと Quantum Protocol が好き。

主にWebサービスの開発を担当
江藤充宏
リクルートグループ新卒入社4年目。スプラトゥーン2のプレイ時間は2100時間超え。

主にWebサービスの開発を担当
柴田悠希
リクルートグループ新卒入社5年目。ビートマニアとセレステが好き。

主にWebサービスの開発を担当
杉森健
リクルートグループ新卒入社4年目。最近ペンシルパズルにはまっています。