はじめに
この記事では、当社内で開発した最適化フレームワークである「 Codable Model Optimizer 」について紹介します。
リクルートでは、機械学習のビジネス活用に長く取り組んできましたが、機械学習によって将来の予測が正確にできたとしても、その予測を元に良い選択を決定できなければならない問題に直面することが増えてきています。 例えば、商品に対する購入率が予測できたとしても、購入率の高い商品をたくさん表出させれば良いというわけではなく、実際には商品の在庫などを考慮してどのように表出させるのか意思決定する必要があります。
膨大な選択肢からより良い選択を見つけ出す問題を"最適化問題"とよび、様々な解法があります。解法としては、数理最適化(主に厳密な最適解を見つけるのに使われる)やメタヒューリスティクス(厳密最適解ではないが、大規模な問題において良い解を見つけるのに使われる)などがあります。
当社内には多様な人材がおり、数理最適化のプロフェッショナルもいます。しかしながら、数理最適化のプロは世の中でも人数が少なく、全ての案件をお願いすることは難しいのが実情です。一方で、ビジネスニーズとして常に厳密な最適解が求められるわけではなく、制約を満たし、安定してそれなりの最適性を持った解を出せれば問題ないケースも多くあります。そこで、リクルートでは、数理最適化のプロではなくてもITエンジニアが気軽に利用できる最適化フレームワークの試作に着手しました。
私たちは2018年から大阪大学の梅谷俊治先生と共同研究を行っており、数理最適化に関する個別案件相談会を定期的に開催しています。 相談会の中で先生から様々なアドバイスをいただき、今回のソルバーを開発することができました。
ソルバーの特徴
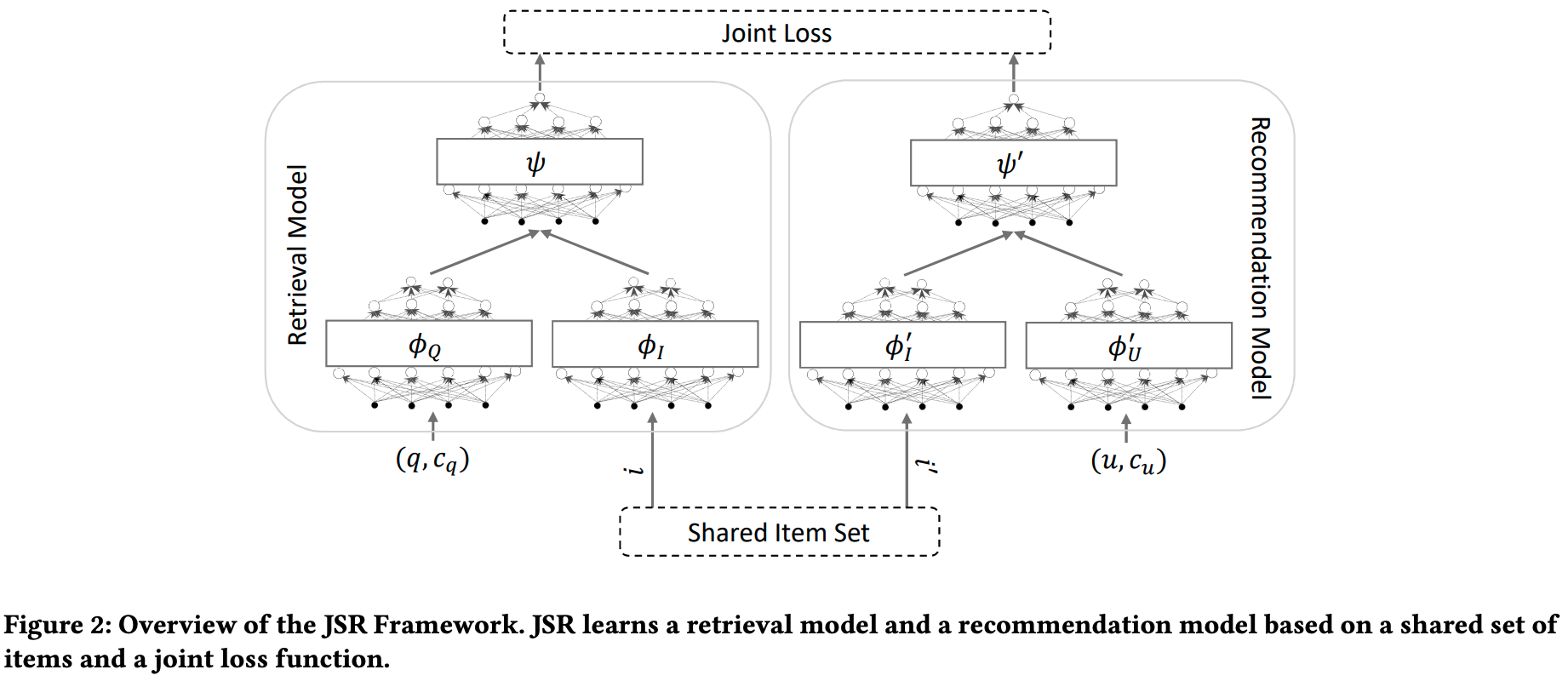
ITエンジニアにとって、数理最適化の難しい要素として、問題のモデル化(定式化)があります。 数理最適化では最大化または最小化したい量を目的関数という関数で表現します。例えば、売り上げを最大化したい場合には、目的関数は売り上げを表現する数式になります。 また、最適化を行う時に満たして欲しい条件を制約として導入します。例えば、投資額がある一定以下の中で売り上げを最大化するという時には、投資額の合計が特定の値より小さいという制約式を導入します。
数理最適化ソルバーを利用するには、これら目的関数と制約式をうまく一次関数の形で表現する必要があるため、ITエンジニアにとっては取っ付きにくい部分があります。また、条件の変更によって、制約が追加されたり、目的関数に新たな要素が少し追加されるだけで、計算時間が急激に増えたり、実行可能解が見つけられなくなることもあり、変更が難しい傾向があります。
一方でメタヒューリスティクスは、最適性の保証までは得られないですが、探索的な手法が用いられることが多く、ITエンジニアにとっては数理最適化より馴染みやすい方法です。ただし、汎用性や拡張性が高く、かつ広く使われているメタヒューリスティクスのためのフレームワークやライブラリは少ないのが現状です。結果、案件ごとにスクラッチで書くケースも多くあります。しかし、スクラッチで書くのは開発に時間もお金もかかり、運用保守にもコストがかかります。
そこで、今回開発したソルバーは上記のような問題を解決するために以下のような特徴を備えました。
- 目的関数や制約式をPythonの関数で定義することが可能。つまり、目的関数の中で別のソルバーや、機械学習の推論器を呼び出すことができる。
- 制約式を追加可、制約に関する重みパラメータも自動調整。
- 変数は、整数型や連続値型の他にカテゴリ値型も提供。
- 最適化エンジンはメタヒューリスティクスベース。必須パラメータはステップ数のみ。
- 利用するメタヒューリスティクスの手法はカスタマイズ可能。
- 全てPythonで書かれており、利用しているライブラリはnumpyのみ、簡単に環境構築可。
一方で、計算速度や最適性については深くは追い求めておらず、一定規模の問題を実用レベルの精度で解けること、または本格実装する前のプロトタイプ作成や基準となる最適化精度の把握に利用できることを目標にしています。
基礎的な使い方
簡単な最適化問題を例にcodable-model-optimizerの使い方を解説します。全ての機能を紹介するわけではないので、詳しく学びたい方は、以下のサイトを参照してください。
インストール
まずライブラリは、pipを使ってインストールできます。
$ pip install codableopt
次にcodable-model-optimizerを使って、最適化問題を解くコードの書き方を解説します。
Problemオブジェクトを生成します。生成時に、引数を用いて、目的関数の最大化/最小化問題の設定を行います。is_max_problem=Trueとした場合は、最大化問題になります。
from codableopt import Problem
problem = Problem(is_max_problem=True)
最適化で利用する変数を定義します。codable-model-optimizerは、整数型・連続値型・カテゴリ型を利用することができます。整数・連続値型では、上界・下界値を設定することができます。カテゴリ値型では、カテゴリ値のとりうる値を文字または数値で設定できます。
from codableopt import IntVariable, DoubleVariable, CategoryVariable
x = IntVariable(name='x', lower=np.double(0), upper=np.double(2))
y = DoubleVariable(name='y', lower=np.double(0.0), upper=None)
z = CategoryVariable(name='z', categories=['a', 'b', 'c'])
目的関数の設定
目的関数は、Pythonの関数と引数のマッピング情報によって定義できます。引数のマッピング情報に、Variableオブジェクトを設定した場合は、Variableオブジェクトの値が渡されます。Variableオブジェクトは、1~3次元配列にしてまとめて渡すことも可能です。また、Variableオブジェクト以外の値やオブジェクトも引数に設定することが可能です。
def objective_function(var_x, var_y, var_z, parameters):
obj_value = parameters['coef_x'] * var_x + parameters['coef_y'] * var_y
if var_z == 'a':
obj_value += 10.0
elif var_z == 'b':
obj_value += 8.0
else:
# var_z == 'c'
obj_value -= 3.0
return obj_value
problem += Objective(objective=objective_function,
args_map={'var_x': x, 'var_y': y, 'var_z': z,
'parameters': {'coef_x': -3.0, 'coef_y': 4.0}})
制約式の設定
制約式は、Variableオブジェクトを含めた不等式をProblemオブジェクトに加えることで定義できます。カテゴリ変数の場合は等式によって特定のカテゴリ値を指定した形で利用する必要があります。(一致する場合は1、一致しない場合は0となる)
problem += 2 * x + 4 * y + 2 <= 8
problem += 2 * x - y + 3 * (z == 'a') + 2 * (z == ('b', 'c')) > 3
ここでz == ('b', 'c')はカテゴリ値zが’b’または’c’の時に1となり、そうでない時には0になる式です。
最適化の実行
最適化を実行するには、Solverオブジェクトを生成し、利用する最適化手法のMethodオブジェクトを引数としてsolve関数に設定し、実行します。実行結果として、“各変数の値のDict"と"実行可能解フラグ"が返ってきます。
from codableopt import OptSolver, PenaltyAdjustmentMethod
# ソルバーを生成
solver = OptSolver()
# 最適化手法を生成
method = PenaltyAdjustmentMethod(steps=40000)
# 最適化実施
answer, is_feasible = solver.solve(problem, method)
最適化手法
codable-model-optimizerがデフォルトで提供しているPenaltyAdjustmentMethodは、重み付き局所探索法(WLS; Weighting Local Search)という手法の一種です。
与えられた制約のもとで、目的関数f(x)を最小化する変数xを探索する問題を考えます。ここで、制約式が違反している時に正の違反量を返すペナルティ関数p(x)を用意します。例えば、2x ≧ 1という制約に対するペナルティ関数はp(x)=(min(2x-1, 0))^2というような形で作成することができます。
ペナルティ関数と重みwの積を目的関数f(x)に加え、評価関数z(x)を以下のように構築します。
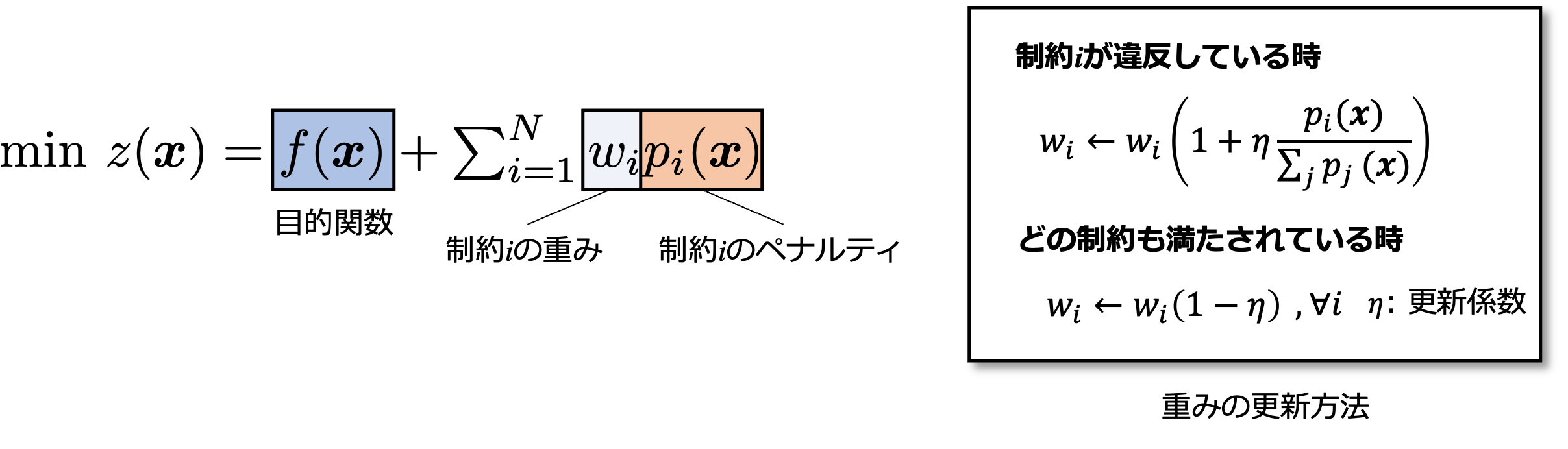
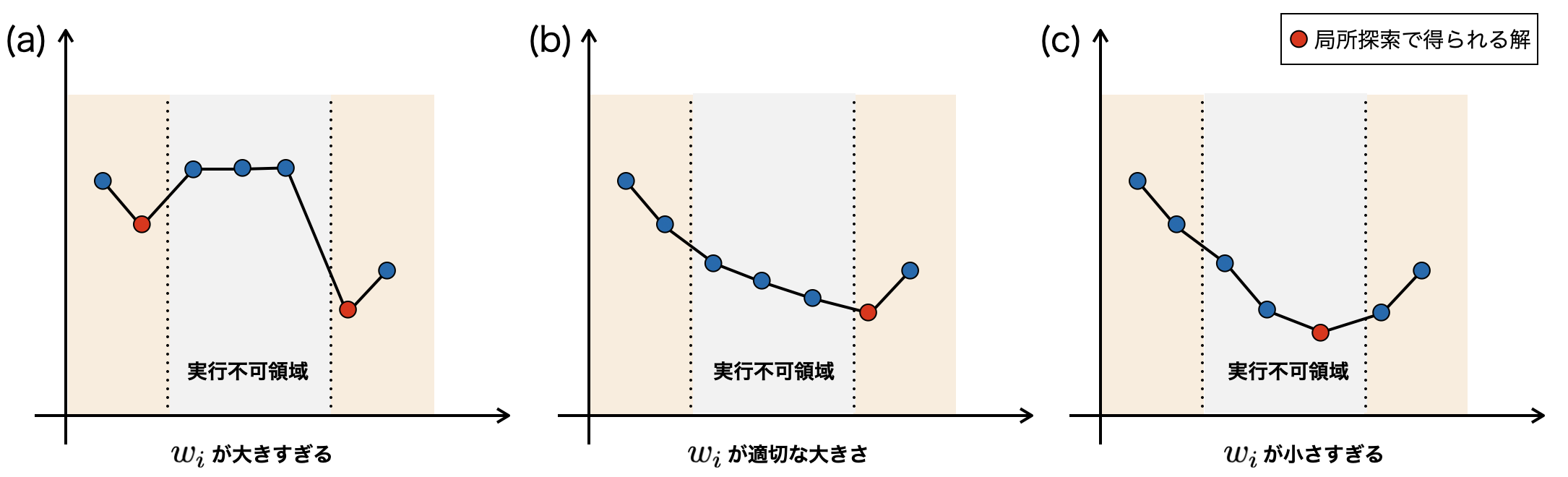
xを少し変化させた時にz(x)が小さくなればその移動を行います。これを繰り返すことでz(x)に対して局所探索を行います。wを調整せずに単に局所探索を行ってしまうと下図(c)のように制約を満たさない解が得られたり、下図(a)の左側の赤丸のように、本来よりも目的関数が良くない解が得られてしまいます。
これを解決するために、ペナルティ重みを適応的に変化させるようにします。ペナルティ重みは、制約違反量が大きいほど大きくします。また、制約式が全て満たされている場合は、一律に全てのペナルティ係数を下げます。このように適応的に重みを変化させることで制約を満たす良い解が得られるようになります。つまり、下図(b)の赤丸のように制約を満たしつつ目的関数が良い解が得られるようになります。(参考文献[2]をもとに図を作成)
この他、解の遷移提案方法等も様々な工夫を施しています。詳細については、
こちら
をご確認ください。
また、もし最適化手法をカスタマイズしたい場合には、OptimizerMethodクラスを継承したクラスを実装することで実現することができます。詳しくは、
こちら
をご確認ください。
[Weighting Local Searchに関する参考文献]
- [1] 柳浦 睦憲, 茨木 俊秀 (著), 組合せ最適化―メタ戦略を中心として―, 朝倉書店
- [2] 梅谷 俊治, A weighting local search algorithm for large-scale binary integer programs
- [3] S. Umetani, Exploiting variable associations to configure efficient local search algorithms in large-scale binary integer programs, European Journal of Operational Research, 263 (2017), 72-81. DOI: 10.1016/j.ejor.2017.05.025 (open access)
- [4] Thornton, J., Clause weighting local search for SAT. Journal of Automated Reasoning, 35, 97–142., 2005
- [5] Nonobe, K., & Ibaraki, T., An improved tabu search method for the weighted constraint satisfaction problem. INFOR, 39, 131–151., 2001
実用例紹介
シェアタクシーの割当問題
本ソルバーは連続値も扱うことができますが、主にはクラスタリングなどの組合せ最適化問題での利用を想定して開発されています。ここではシンプルなシェアタクシーの割当問題を例にして紹介します。
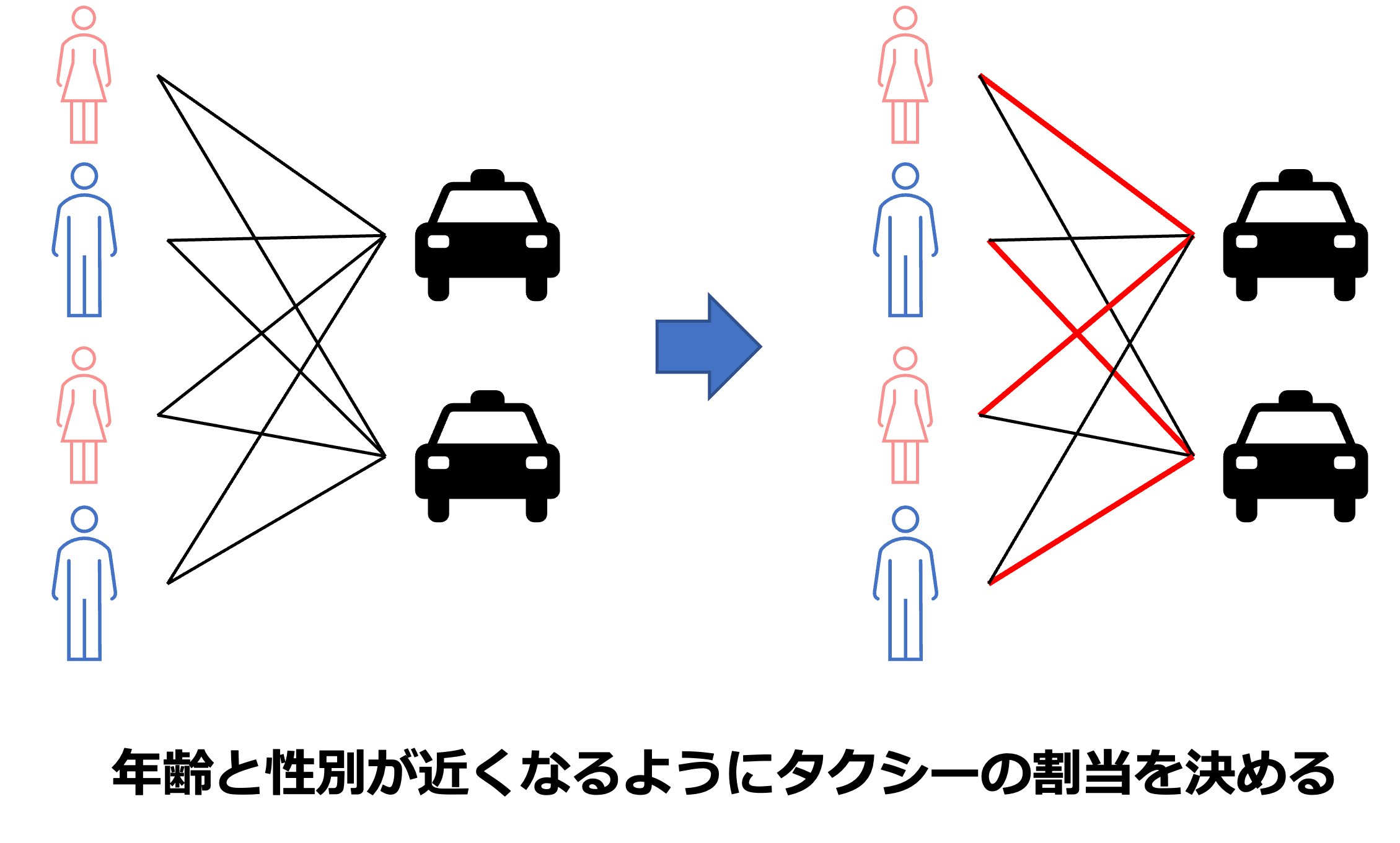
出発時間と出発地と目的地がおおよそ同じである顧客が30人おり、この顧客を10台のタクシーに割り当てます。各タクシーに乗れる人数は4人までです。なるべく年齢や性別が同じ人が割り当てを選択する最適化問題です。問題定義のサンプルコードは下記のようになります。(Github上のコードは、 こちら です。)
# 顧客名とタクシー名を生成
customer_names = [f'CUS_{i}' for i in range(30)]
taxi_names = [f'TAXI_{i}' for i in range(10)]
# 顧客の年齢、性別をランダムに生成
customers_age = [random.choice(['20-30', '30-60', '60-']) for _ in customer_names]
customers_sex = [random.choice(['m', 'f']) for _ in customer_names]
# 顧客の車割り当て変数を作成
x = [CategoryVariable(name=x, categories=taxi_names) for x in customer_names]
# 問題を生成
problem = Problem(is_max_problem=True)
# タクシー内の乗客の年代や性別が同じ人が多いほどスコアが高くなる目的関数
def calc_matching_score(var_x, para_taxi_names, para_customers_age, para_customers_sex):
score = 0
for para_taxi_name in para_taxi_names:
customers_in_taxi = [(age, sex) for var_bit_x, age, sex
in zip(var_x, para_customers_age, para_customers_sex)
if var_bit_x == para_taxi_name]
num_in_taxi = len(customers_in_taxi)
if num_in_taxi > 1:
# タクシー毎の乗客数と年代/性別の種類数の差分をスコアとする
score += num_in_taxi - len(set([age for age, _ in customers_in_taxi]))
score += num_in_taxi - len(set([sex for _, sex in customers_in_taxi]))
return score
# 目的関数を定義
problem += Objective(objective=calc_matching_score,
args_map={'var_x': x,
'para_taxi_names': taxi_names,
'para_customers_age': customers_age,
'para_customers_sex': customers_sex})
# 1台あたりのタクシーに乗れる人数は4人以下である制約式を追加
for taxi_name in taxi_names:
problem += sum([(bit_x == taxi_name) for bit_x in x]) <= 4
このように、codable-model-optimizerを利用するとカテゴリ変数や目的関数を式ではなく関数で表現できるので、直観的に書くことができます。実際のタクシーのシェアリング問題では、出発地点や目的地点、時間帯や顧客毎の希望条件など複雑なニーズがあり、サンプルコード以上に式で表現することは難しくなりますが、本ソルバーであれば簡単に表現することができます。
機械学習の推論処理を目的関数の計算で使う
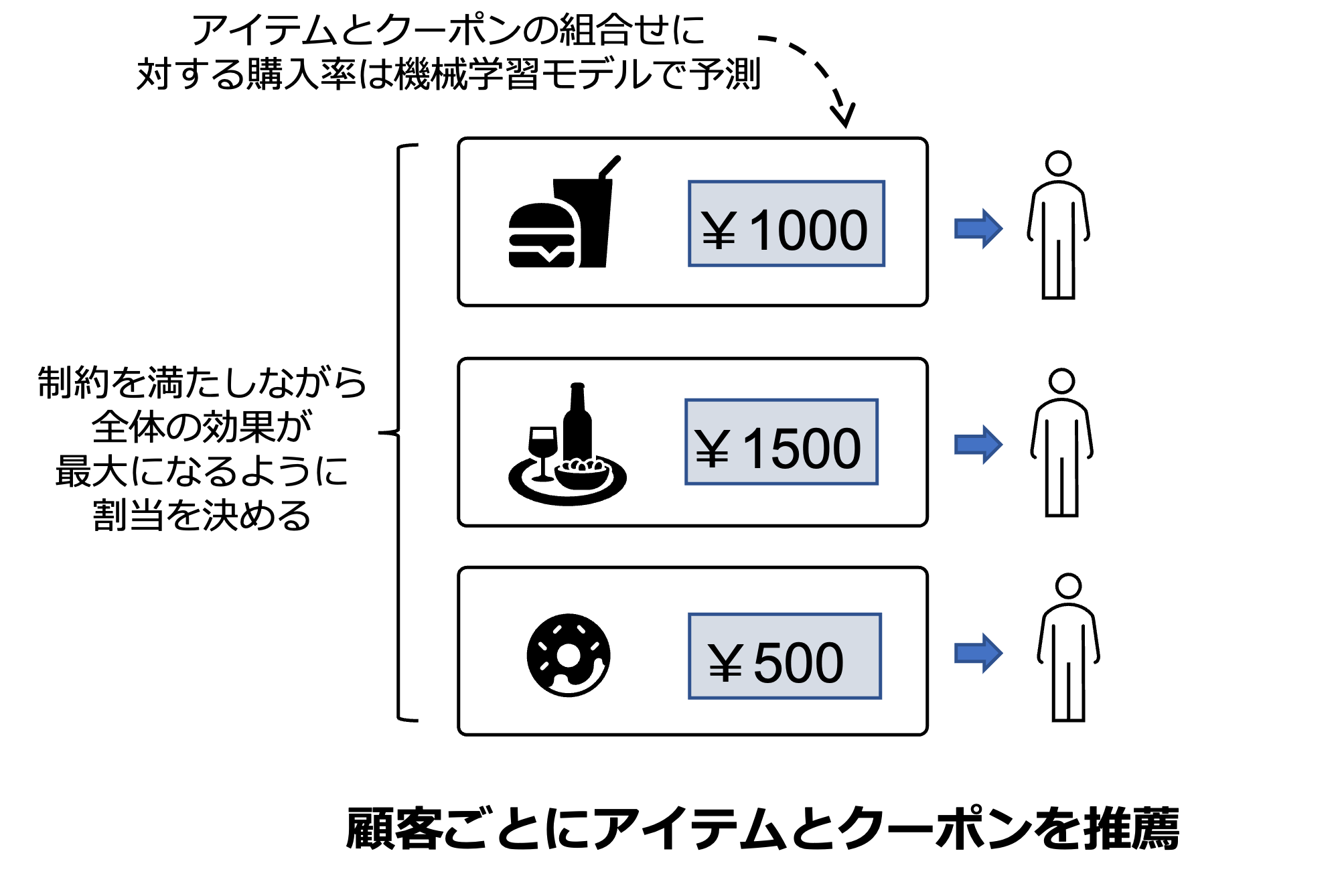
また、codable-model-optimizerは機械学習モデルの出力を目的関数の計算に利用することができます。通常のソルバーでは、機械学習モデルの出力パターンを網羅的に事前計算する必要がありますが、出力パターンが組合せ爆発し、膨大な計算量やメモリ量が必要になる場合があります。一方で、本ソルバーであれば目的関数内で機械学習モデルを呼び出すことができるので、このような問題は発生しません。レコメンドアイテムの選択問題を例を使って説明します。
Webなどのレコメンドにおいては、行列分解や勾配ブースティングなど機械学習モデルの出した関連度スコアの高い順にアイテムを割り当てることが多いですが、在庫が有限である特定の人気商品にクリックが偏る問題や、合わせてクーポンの最適化をしたいケースなどもあり、このような場合には最適化を使って割り当てを決定することがあります。以下のサンプル問題は、期待利益金額が最大化するように、顧客毎にレコメンドする商品と割引クーポンの組合せを決定する問題です。期待利益金額は、機械学習モデルによって顧客と商品と割引金額から購買確率を計算し、商品と割引金額から計算した利益金額を掛け合わせて計算します。目的関数のサンプルコードは以下のようになります。(Github上のコードは、 こちら です。)
# 利益の期待値を計算する関数、目的関数に利用
def calculate_benefit(
var_selected_items: List[str],
var_selected_coupons: List[str],
para_customer_features_df: pd.DataFrame,
para_item_features_df: pd.DataFrame,
para_coupon_features_df: pd.DataFrame,
para_model):
df = pd.concat([
para_customer_features_df.reset_index(drop=True),
para_item_features_df.loc[var_selected_items, :].reset_index(drop=True),
para_coupon_features_df.loc[var_selected_coupons, :].reset_index(drop=True)
], axis=1)
# 引数で渡した機械学習モデル(para_model)を利用して購買確率を計算
buy_rate = \
[x[1] for x in para_model.predict_proba(df.drop(columns='item_cost'))]
# 利益を計算
profit = df['item_price'] - df['item_cost'] - df['coupon_down_price']
# 総利益の期待値を計算
return sum(buy_rate * profit)
このように、codable-model-optimizerは引数に機械学習モデルを組み込んだ目的関数も簡単に定義することもできます。これも先ほど同様に目的関数をPythonの関数として表現でき、さらに引数を自由に設定できる機能の利点となります。
最適化問題の問題分割に利用する
codable-model-optimizerは、既存のソルバーを生かした方法でも利用することができます。今回は、マルチデポの容量制約有りの配送計画問題を例に紹介します。(Github上のコードは、 こちら です。)
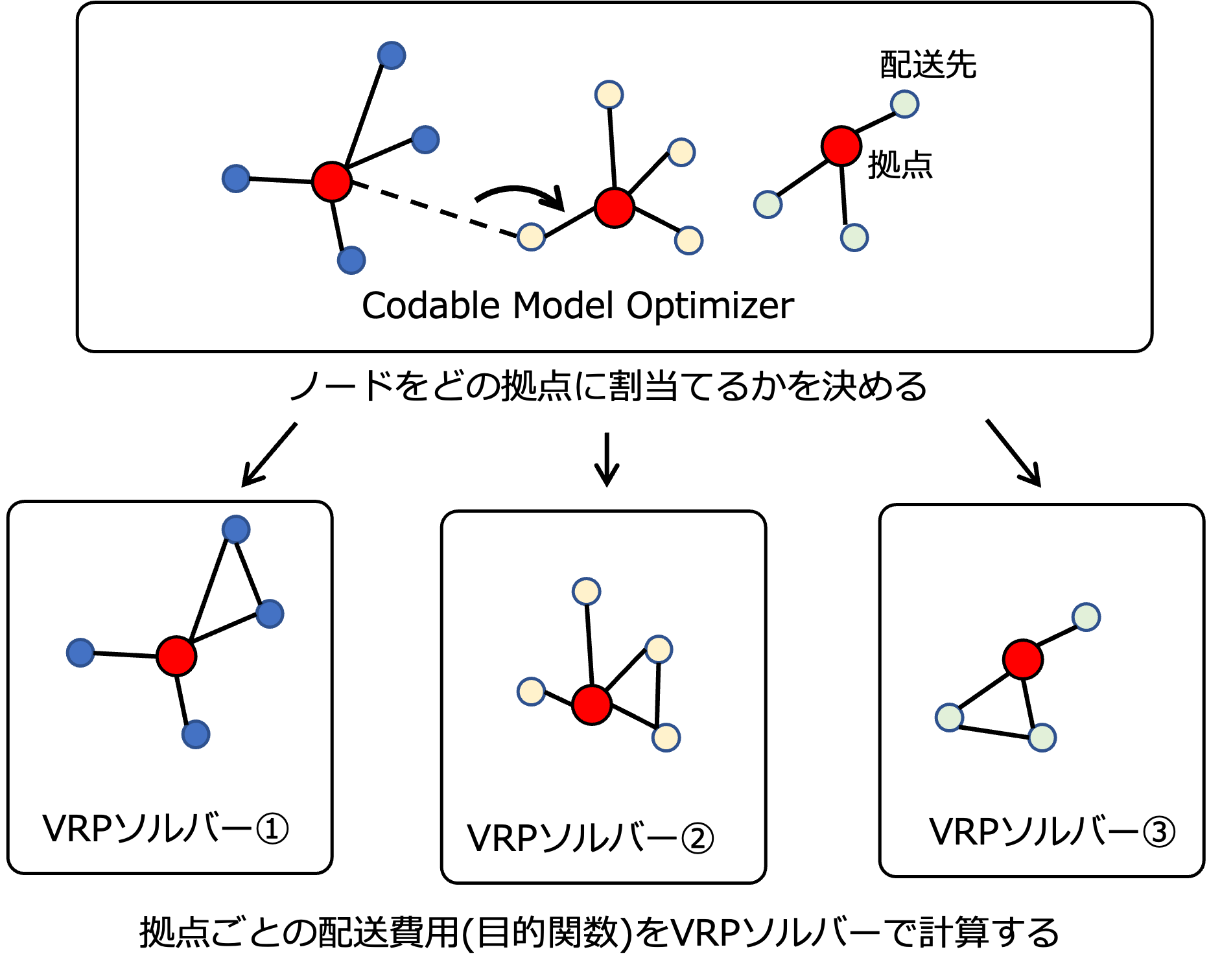
配送計画問題は、様々な形式の問題があり、多くの問題が数理最適化によって厳密解を得るのが非常に困難です。特に規模の大きな問題になるほど、必要となる計算時間が膨大になるため、問題分割を利用して解いた方が良い場合があります。本サンプル問題では、マルチデポの配送計画問題をデポ毎の配送計画問題に分割して解いています。
サンプル問題では、各デポからの配送先を決定し、そのルートを最小化する問題を取り扱っています。配送先には荷物をどのデポから送っても問題ありません。さらに、各デポには取り扱える配送総量の上限があります。また、各デポから配送トラックは何台でも出ることができますが、トラックの積載制約があります。
ここでのcodable-model-optimizerの役割は、各デポの配送先を確定することです。この時、合わせて各デポが扱える配送総量の上限についても考慮しています。各デポの配送先を確定した後は、既存のソルバーでデポ毎に容量制約有りの配送計画問題を解き、全ての配送ルートの距離を計算しています。
このサンプルコードでは、その他にも計算を効率化するためのテクニックが2つ利用されています。
- キャッシュオブジェクト(cashed_part_obj)の導入: 問題分割した配送計画問題の結果をキャッシュし、再度必要になった場合はキャッシュを参照することで、分割した配送計画問題を再度解かないようにしています。
- より良い初期解の指定: codable-model-optimizerは、solve関数を呼び出す際に、初期解をinit_answersとして指定することができます。初期解は複数指定でき、それぞれの初期解で最適化を繰り返し行います。サンプルコードでは、各配送先が一番近いデポを選択するルールベースで作成した解を初期解に指定することで、効率的な探索を実現しています。
mdcvr_problem = MultiDepotCVRProblem.generate(depot_num=8, place_num=40)
opt_problem = Problem(is_max_problem=False)
x = [CategoryVariable(name=x, categories=[y for y in problem.depot_names])
for x in problem.place_names]
def calc_obj(var_x, para_problem: MultiDepotCVRProblem, cashed_part_obj: Dict[str, float]):
obj = 0
for depot_no, depot_name in enumerate(para_problem.depot_names):
place_noes = [place_no for place_no, val in enumerate(var_x) if val == depot_name]
if len(place_noes) > 0:
child_problem = para_problem.to_child_problem(depot_no=depot_no,
place_noes=place_noes)
cash_key = depot_name + '_' + '_'.join([str(x) for x in place_noes])
if cash_key in cashed_part_obj.keys():
# キャッシュから子問題の目的関数値を取得
part_obj = cashed_part_obj[cash_key]
else:
# 子問題の目的関数値を計算
part_obj = CVRPSolver.solve(child_problem)
# 差分計算用にキャッシュ
cashed_part_obj[cash_key] = part_obj
else:
part_obj = 0
obj += part_obj
return obj
opt_problem += Objective(objective=MultiDepotCVRPSolver.calc_obj,
args_map={'var_x': x,
'para_problem': problem,
'cashed_part_obj': {}})
# デポの容量制限の制約式
for depot_name in problem.depot_names:
opt_problem += \
sum([(bit_x == depot_name) * problem.demands[bit_x.name] for bit_x in x]) <= \
problem.depot_capacities[depot_name]
# 初期解生成(各配送先が一番近いデポに割り当てられる解を生成)
init_answer = MultiDepotCVRPSolver.generate_init_answer(problem)
solver = OptSolver(debug=True, debug_unit_step=100, num_to_tune_penalty=10)
method = PenaltyAdjustmentMethod(steps=1000)
# 初期解設定(各配送先が一番近いデポに割り当てられる解を生成)
dict_answer, is_feasible = solver.solve(opt_problem, method, init_answers=[init_answer])
最後に、実際にサンプルデータを用いた最適化の結果を確認してみましょう。問題パラメータは下記の通りです。
- デポ数: 8
- 配送先数: 40
- デポの配送総量の上限: 112 ~ 232
- 配送先の配送量: 10 ~ 50
- トラックの積載制限: 100
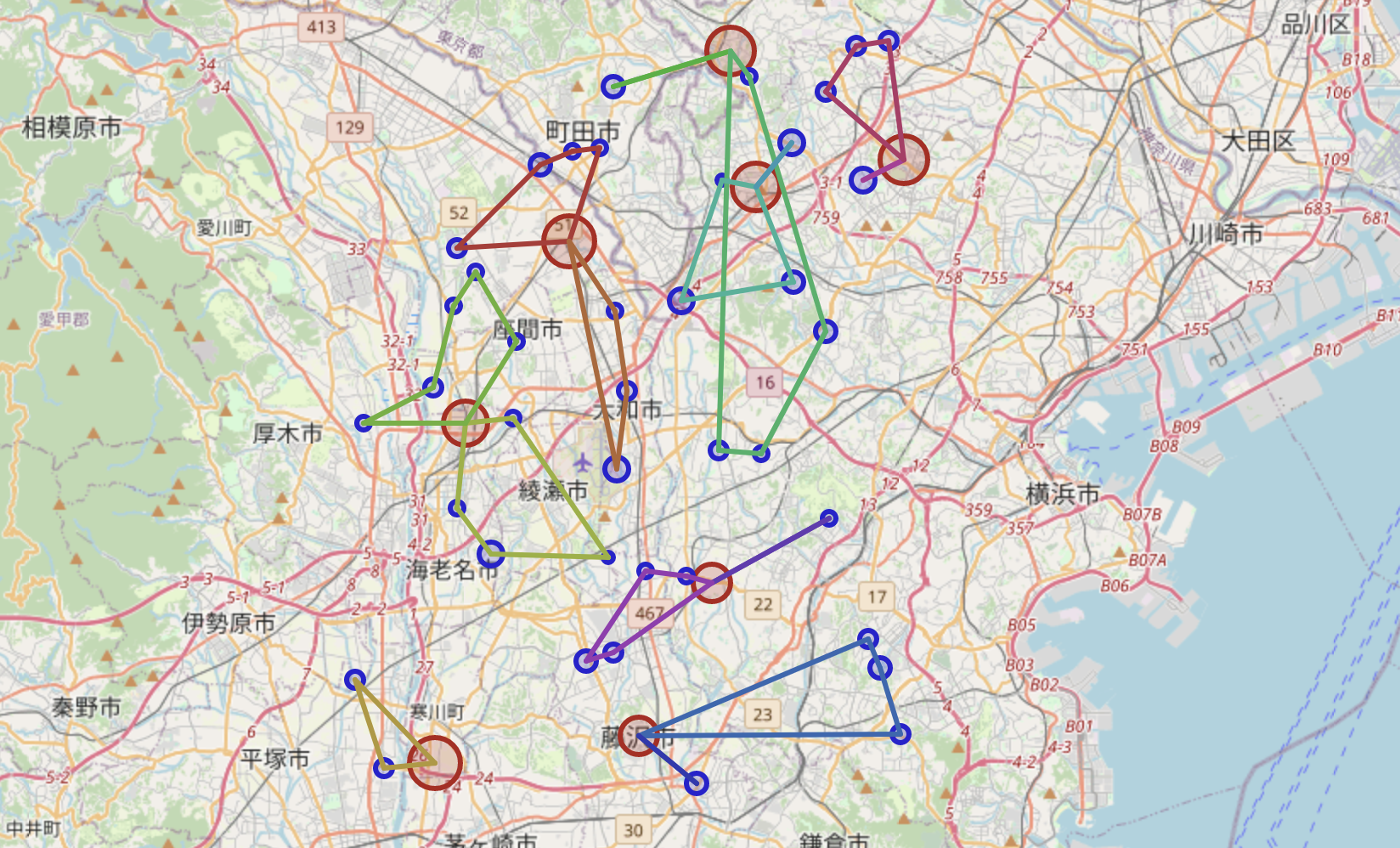
上の図は、解のルートを記した地図です。地図上の赤い丸がデポ、青い丸が配送先、線が配送ルートを表しています。また、丸の大きさは「デポの配送総量の上限」や「配送先の配送量」の大きさを表しています。なるべく近くのデポからまとめて配送する解になっていますが、各デポの配送総量の上限から一部はやや遠いデポから運ばれている傾向が見えます。
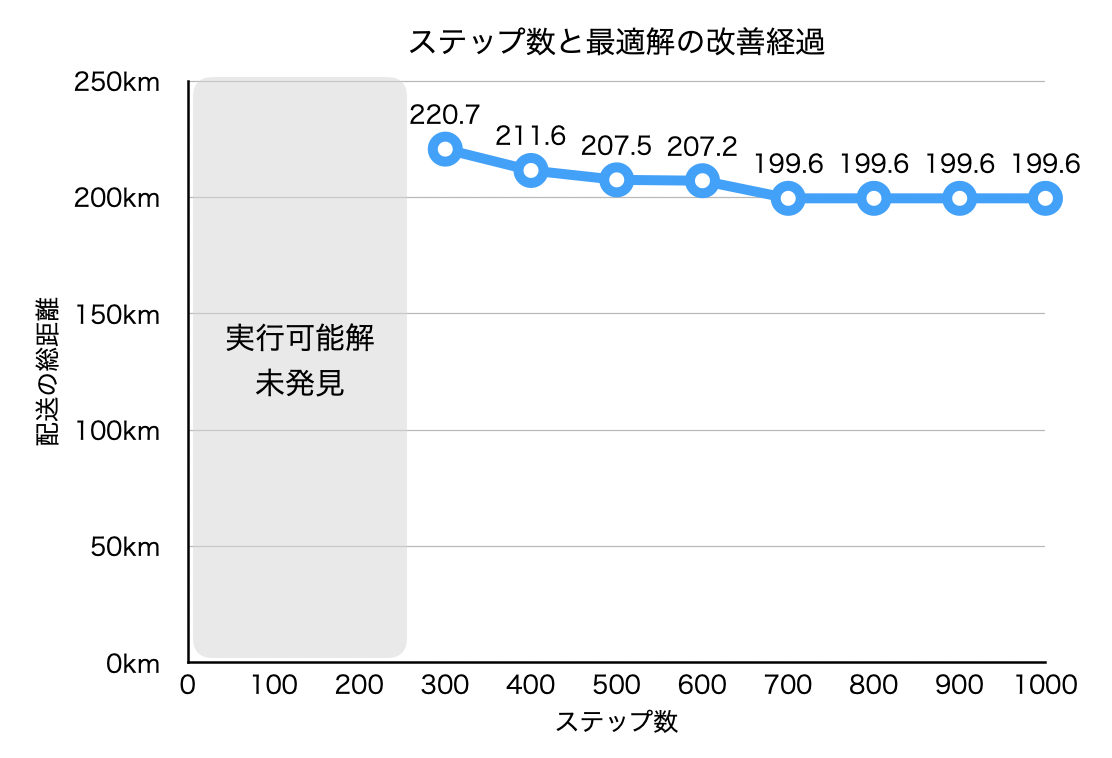
上の図は、ステップ数毎の目的関数値の変化を示したグラフです。最初は、ルールベースの解が制約を満たしていないため実行可能解が見つかっていませんが、codable-model-optimizerが配送先とデポの割当を変更していくことでステップ数が300の時点で実行可能解を発見していることが分かります。また、さらにステップ数が700になるまで目的関数を改善していることが読み取れます。
終わりに
本記事では、開発したcodable-model-optimizerの紹介をしました。この他にも紹介していない機能がありますが、 ドキュメント をご覧下さい。 簡単に利用できる最適化ソルバーを目指し開発したものですので、ぜひ試しに利用してみてください。

ソフトウェアエンジニア
Motohashi & Tanahashi
Codable Model Optimizerの開発など、ビジネス課題を最適化で解決するための方法を考えています。