長期報酬に対する逐次的オフ方策学習(半熟仮想株式会社との共同研究)

はじめに

初めまして。アドバンスドテクノロジーラボ(通称ATL)の吉住宗朔とビューティーデータサイエンスグループの池田春之介です。本日は先日日本オペレーションズ・リサーチ学会で発表した「⻑期報酬に対する逐次的オフ方策学習」について紹介したいと思います。 (この研究は半熟仮想株式会社の齋藤優太さんとの共同研究です。共同研究の経緯/概要についてはこちらのエントリでも紹介しています)

背景

案件背景

クーポンやポイントなどのインセンティブ施策を行うマーケターは「限られた予算で売上を最大化するためにはどうすれば良いか？」を考えています。その手段の一つとしてインセンティブの効果がありそうな人を推定して、その人たちにインセンティブを配布するパーソナライズ施策があります。その際、実際にABテストなどで効果を測定する前に、 ロジックの良し悪しを現状手元にあるデータで評価/最適化したい(オフ方策評価/学習) と言う欲求があります。

技術背景

IPS推定量

オフ方策評価の代表例として、介入の逆確率で報酬を補正するIPS（Inverse Propensity Score）推定量を使う方法があります。 IPS推定量は下記のように記号を定義すると以下のように書けます。

記号	意味
$x_i$	ユーザー$i$の特徴量。過去の購買履歴など。
$r_i$	ユーザー$i$の報酬。売上など。
$a_i$	ユーザー$i$の介入。インセンティブの種類など。
$\pi_0(a_{i}\|x_i)$	手元のデータにあるデータを取得する時の方策。$a_i$を選択する確率。
$\pi_\theta(a_{i}\|x_i)$	評価したい方策。

$$ \hat{V}(\pi_{\theta}) = \frac{1}{n} \sum_{i=1}^{n} \frac{\pi_\theta(a_{i,t}|x_i)} {\pi_0(a_{i,t}|x_i)} r_i $$

この式は元のデータであまり現れていない($\pi_0$の小さい)介入を大きく評価しており、データ取得時に発生したバイアスを除外することが出来ます。 (例えば、ある病気を予防するためのワクチンが高齢者を中心に接種されていたとして、そのまま集計すると高齢者に偏った効果が計測されてしまうので、データ量の少ない若者のデータを水増しして集計するイメージ) しかし、少ないデータを拡大推計しているので、推定量のバリアンス(分散)は大きくなってしまいます。

方策勾配法

上記の推定量を最大化する方策は方策勾配法によって求められます。具体的には、方策のパラメータ$\theta$は、学習率を$\eta$として以下の更新を繰り返すことで求めることが出来ます。

$$ \theta_{h+1} \leftarrow \theta_h + \eta \nabla_{\theta_h} V(\pi_{\theta_t}) $$

今回の課題

これまで考えられていたインセンティブのパーソナライズは1期間の施策でした。つまり、考えている期間で報酬が得られるかが重要であり、次の期に及ぼす影響が考慮できていませんでした。しかし、インセンティブ施策では予約の先食い(インセンティブによって予約するがその後の予約はないこと)や定着(インセンティブによって予約してその後も予約するようになること)などを考慮することは重要です。

これに対応するためには、多期間の介入を最適化しなければなりません。しかし、多期間の介入を考えると検討すべきパターン数が膨大になります。(例えば、1ヶ月の介入が2パターンだとしても、12ヶ月の介入を考えるとパターンが各月2つずつあるので、2^12=4096パターンになる) 介入パターンが多過ぎると、$\pi_0$と$\pi_\theta$が異なりやすく、IPS推定量のバリアンスが大きくなってしまうと言う問題点があります。そこで、介入パターンが多い多期間のインセンティブ施策について、オフ方策評価/学習をする手法を作りたい、と言うのが本研究の目的になります。

問題設定

今回は多期間の介入の最適化を考えます。そのために以下のような設定を考えます。

$t$期の最適化ではなく、$t$期〜$t+T$期までの最適化を考える。
介入は$a_t$ではなく、$t$期〜$t+T$期までの介入$a_{t:t+T}$を最適化する。
その際の報酬は$r_t$ではなく、$t$期〜$t+T$期までの報酬の合計を$R_{t+T}$とする。

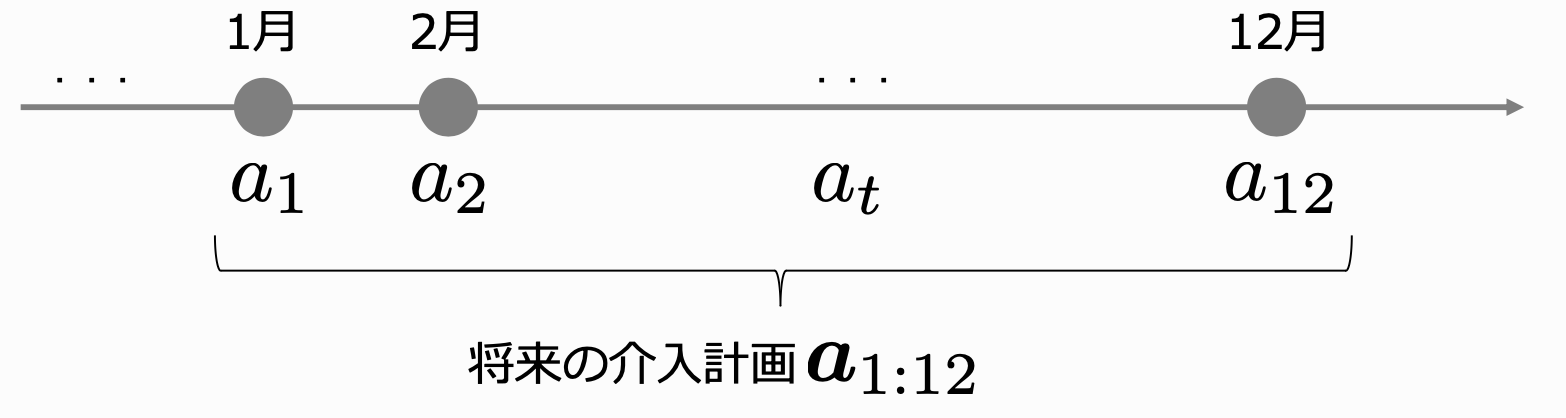
今回考える多期間の報酬に関するIPS推定量は $R_{i, t} = \sum_{t'=t-T}^{t} r_{i,t'}$ として、以下のように書けます。 (手元の過去データを元に推定するため、$t-T$期〜$t$期のデータを用いて推定していることに注意)

$$ \hat{V_l}(\pi_{\theta}) = \frac{1}{n} \sum_{i=1}^{n} \frac{\pi_\theta(a_{i,t-T:t}|x_i)} {\pi_0(a_{i,t-T:t}|x_i)} R_{i,t} $$

このような問題設定では、介入のパターンが$T$乗のオーダーで増えてしまうため、期間を延ばせば延ばすほどパターン数が爆発的に増えてしまいます。

提案手法

OFFCEM推定量

介入のパターンが多すぎる問題に対処するために、今回は OffCEM(Off-Policy Evaluation for Large Action Spaces via Conjunct Effect Modeling) と言う推定量を使います。 CEMでは、以下の式で期待報酬関数$\hat{f}(x, a)$をクラスター効果$g(x, c(x, a))$と残差効果$ h(x, a)$の和として表します。

$$ \hat{f}(x, a) = \hat{g}(x, c(x, a)) + \hat{h}(x, a) $$

上記$\hat{f}$を用いて、OffCEM推定量は以下のように定義されます。

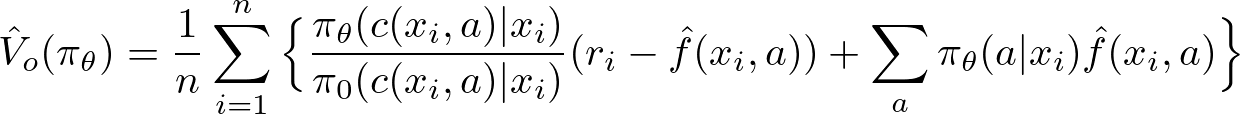
この推定量の利点は、第一項はクラスター効果として比較的低バリアンスでバイアスの無い推定が出来るところです。そして、クラスター効果で考慮できなかった部分については、第二項でIPSによる重みづけを行わないことで、バイアスは発生しますがバリアンスを抑えることができます。

また、今回の提案手法ではクラスタの定義を$c(x, a) = a_{t:t+k}$としています。つまり、単純に直近$k$期間の介入をクラスタとしています。この推定量は$k$が大きいほどバイアスは減少していきますが、バリアンスは増加します。そして、$k=T$とすると通常のIPS推定量と一致します。したがって、適切な$k$の値を設定することで、長期的な効果を考慮しつつ、バリアンスを改善することが可能です。

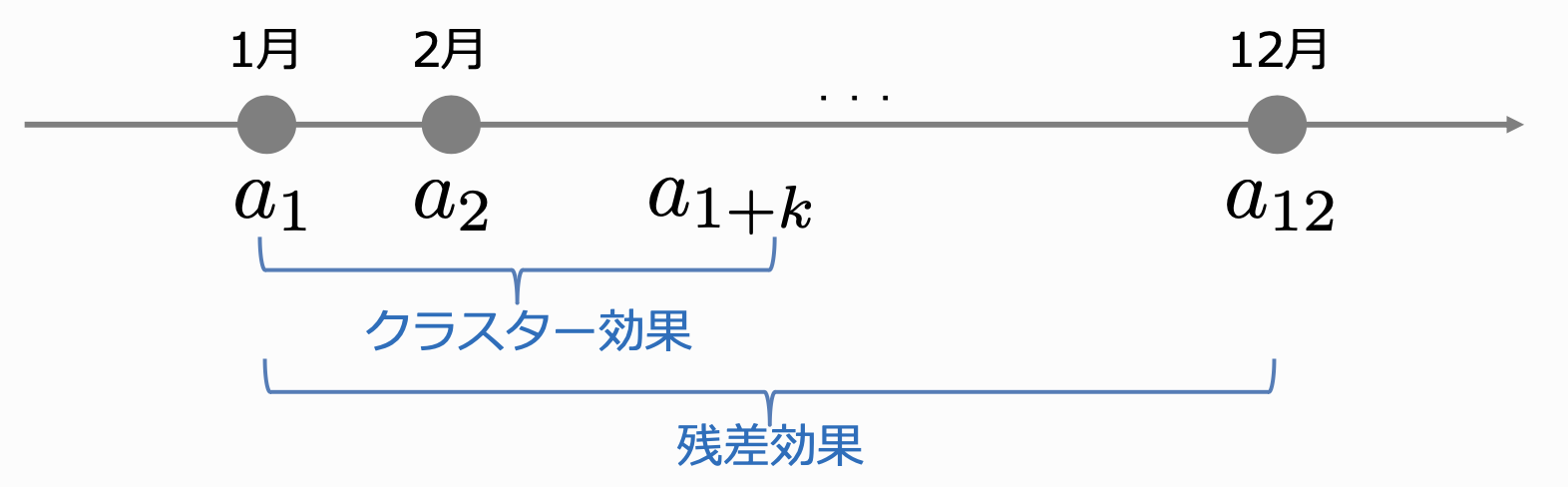
Receding-Horizon最適化

上記の方策では$k$期分の介入計画がまとめて出力されます。しかし、実際の問題に適用する場合は$t$期に対して介入を行い、$t+1$期には$t$期の結果を踏まえて計画を変えられるので、$t$期に将来の計画を全て守る必要はありません。 Receding-Horizon最適化では、$t$期において$k$期先までの介入計画を最適化する行動を決定しますが、実際に介入を行うのは最初の$t$期のみで、次の期ではまた$k$期先までの介入計画を最適化します。 Receding-Horizon最適化を行うことで、将来の介入計画も考慮しつつ、各期でのログデータも有効に活用することが出来ます。

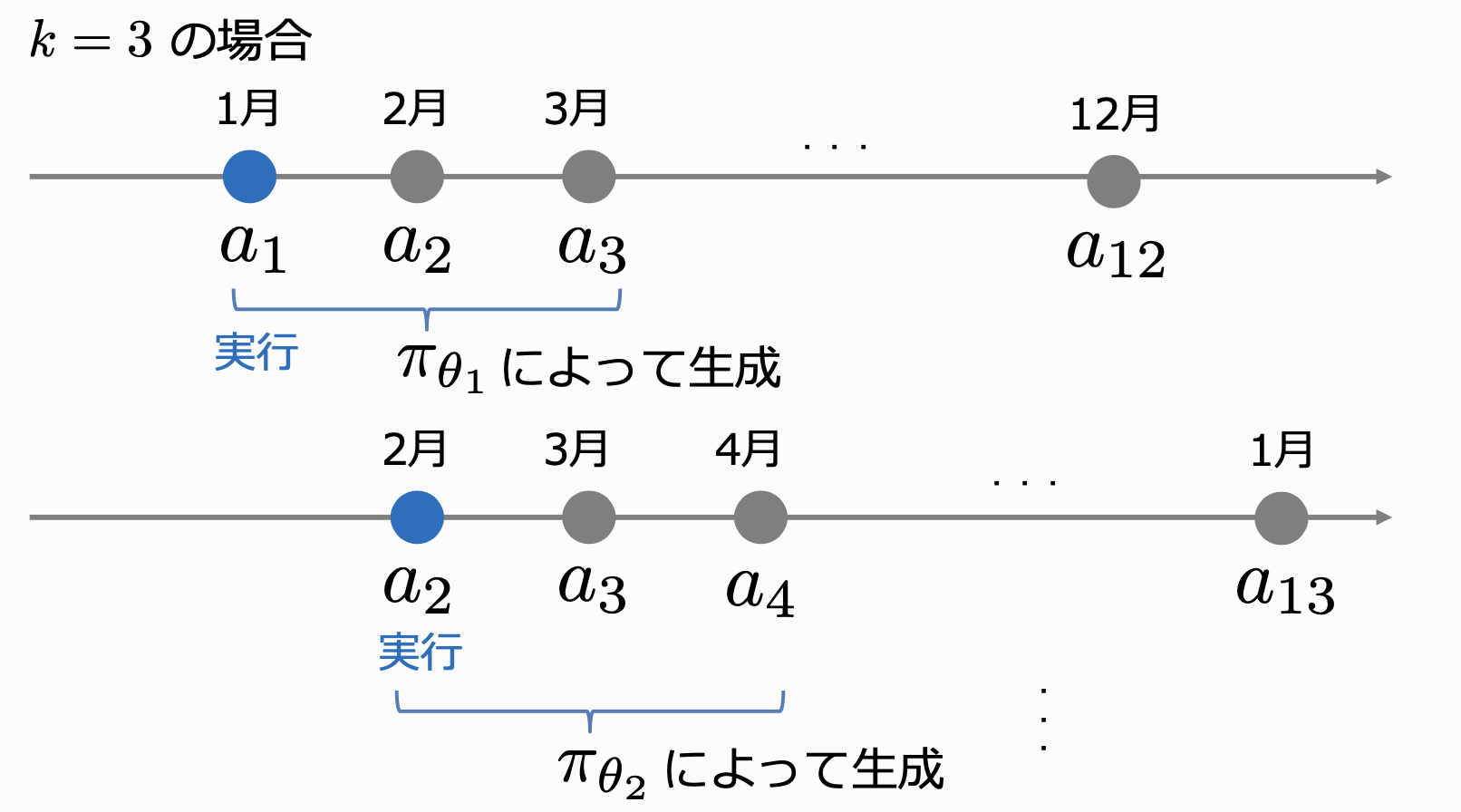
また、具体的な手順は以下のようになります。

各期$ t \in T $で以下の処理を繰り返す。
1. ログデータ $ D_t $ を用いて $ k $ 時点での方策 $ \pi_{0,t} (a_{t:t+k} | x) $ 方策勾配法を用いて学習する。
2. 方策 $ \pi_{0,t} (a_{t:t+k} | x) $ から行動 $ a_{t:t+k} $ を抽出し、最初の $ a_t $ のみ実行する。
3. 新たなログデータ $ D_t :={ (x_i, t, a_i, t, r_i, t)^{n_t}_{i=1}} $ を観測する。

数値実験

人工データによる数値実験の結果を紹介します。細かい設定は省略するのですが、真の報酬関数やユーザーの特徴量を乱数で生成し、通常のIPSを用いて学習した方策と今回の提案手法を用いて学習した方策で期待報酬の値を比較します。方策は方策勾配法で学習しています。結果は以下のようになりました。

各期の行動数	期間	全期間の行動数	通常のIPSを100%とした場合の期待報酬
2	5	32	98.6%
2	7	128	105.5%
2	9	512	121.4%

これを見ると行動数が少ない場合は通常のIPSとあまり変わらない精度になっていますが、行動数が増えるに従って期待報酬が高まっていることがわかります。そのため、 提案手法は多期間の最適化のような介入のパターンが多い問題に対して有効である と考えられます。

おわりに

最後までお読みいただきありがとうございました。長期効果の考慮はインセンティブ施策の長年の課題だったので、解決の糸口が見えたことは大きな進歩だったと思います。課題感はあったものの社内の人間だけでは定式化するところまでは難しく、これは半熟仮想株式会社の齋藤さんと共同研究していなければ成し遂げられないことだったと思います。現在は人工データでの数値実験の段階ですが、これから実データでのオフライン/オンライン検証や手法の改善をやっていきたいと考えています。

リクルートでは本件以外でも大学を初めとする研究機関とも共同研究が行われており、働きながら技術的な研鑽を積むことや、対外発表などの活動も可能です。ご興味のある方は、以下の採用ページをご覧ください。