はじめに

はじめまして、2023年10月にシニアリサーチャーとして入社したアドバンスドテクノロジーラボ（ATL）の梅谷俊治です。2023年9月まで、大阪大学大学院情報科学研究科にて数理最適化寄附講座教授を務めていました。 本記事では、リクルートのデータ推進室における数理最適化を活用した問題解決の取り組みをご紹介します。

数理最適化は、与えられた制約条件の下で、目的関数を最小（もしくは最大）にする最適化問題を通じて、現代社会における意思決定や問題解決を実現する数理技術の一つです。 近年では、機械学習によるデータ分析や予測の技術開発が進み次々と実用化されています。数理最適化は、それらのデータ分析や予測の結果を踏まえた上で意思決定や計画策定を実現する問題解決における出口を担当する技術です。例えば、オンライン広告などカスタマーに商品を推薦するレコメンデーションでは、機械学習を活用してカスタマーの商品に対する期待利得を推定できても、直ぐにサービスが実現できるわけではありません。予算やクライアントの意向を考慮した上で、一部の人気商品や敏感なカスタマーに偏らないように上手く商品を推薦するためには、大規模な最適化問題を解く必要が生じます。 このように、機械学習によるデータ分析や予測の技術の普及にともない、製造業や物流業にとどまらない幅広い分野における現実問題の多くが最適化問題に定式化できることが再認識されるようになりました。また、現在では、有償・無償を含めて多くの数理最適化ソルバー（最適化問題を解くソフトウェア）が利用できるようになり、現実問題を解決するための有用な手段として急速に普及しつつあります。

最近は、多くの企業が数理最適化の活用に強い関心を持つようになり、大学においても企業との共同研究など産学連携の機会が急増しています。しかし、企業に数理最適化の専門家は少なく、大学から輩出できる人材にも限りがあるため、実務における数理最適化の活用はごく限定的な範囲に留まっているのが現状です。 この課題を解決するため、（１）実務の各段階における問題解決の支援を通じて数理最適化の専門家を育成し、基幹事業に数理最適化を活用する枠組みを創出すること、（２）産業や学術の幅広い現実問題に迅速に対応するための基盤技術となる、高性能かつ汎用的な数理最適化ソルバーを開発することを目標に活動しています。

数理最適化を活用した問題解決の実現

最適化の理論やアルゴリズムの専門知識があれば、現実問題が即座に解決できるわけではなく、実際には、最適化問題の定式化にかかる現場担当者のインタビューからシステムの開発・導入にいたるまで、これらの専門知識だけでは解決できない課題が数多く存在します。

例えば、最適化問題の定式化に必要な情報の多くは、日常的に特定の業務に従事している現場担当者にとって改めて話題にするまでもない常識であり、優秀なコンサルタントが慎重なインタビューを重ねてもこれらの情報を引き出すことはなお困難です。そのため、コンサルタントは最適化問題が上手く定式化できないまま次の段階に進まざるを得ず、提示した計画案が現場担当者の期待から大きく外れてしまうことは少なくありません。これは、現場担当者とコンサルタントのどちらか一方が悪いわけではありません。そもそも、現場担当者が最適化問題の定式化に必要な情報を自ら整理できるならばコンサルタントは不要なはずです。むしろ、不十分でも暫定的な計画案を提示することは、現場担当者から有用な情報を引き出すための手段だと割り切ることが望ましいです。

記事¹では、数理最適化の専門家が現実問題に取り組む際に生じる課題とその対策をまとめました。記事²³では、リクルートにおいて数理最適化を活用した産学連携の取り組みと事例を紹介しています。また、これらの成果を国内外の学会で発表しています。以下では、国内外の学会で発表した取り組みの一部を紹介します。

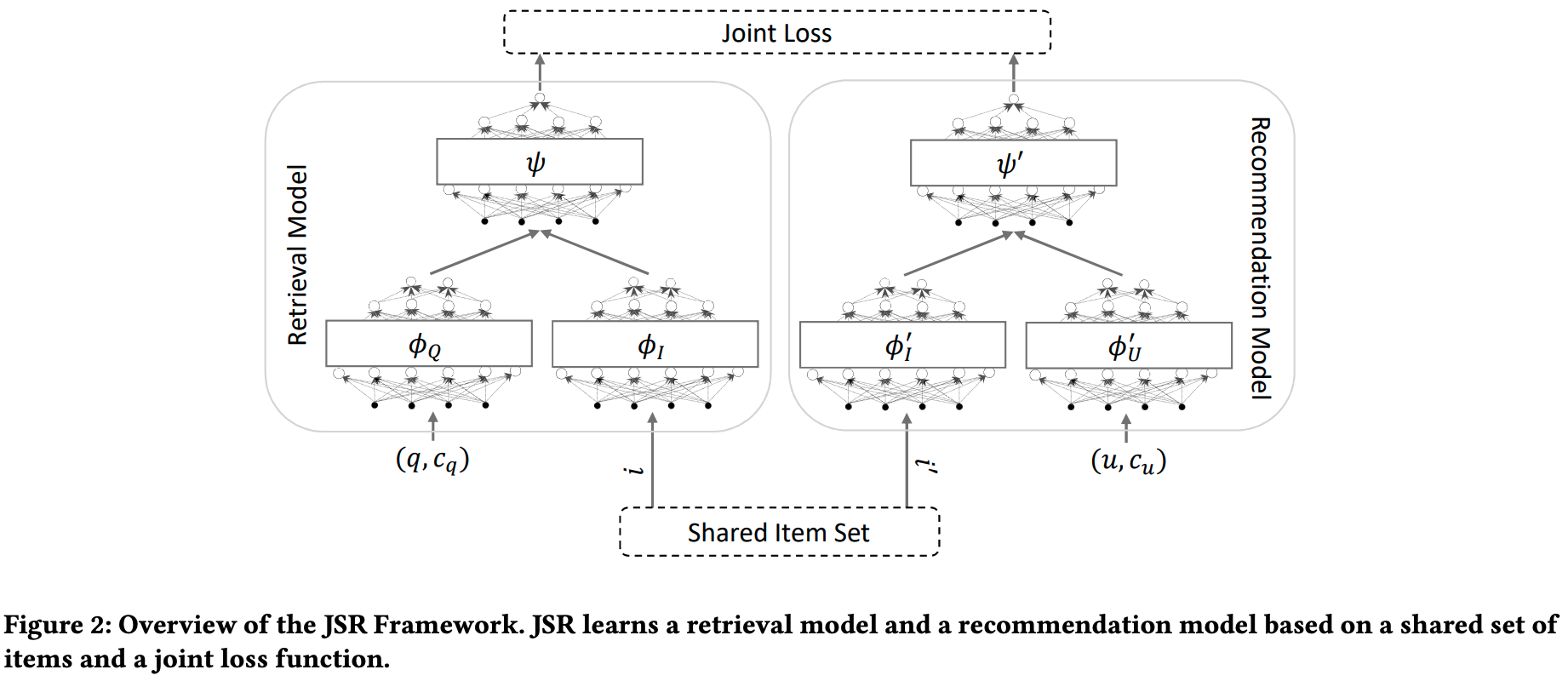
レコメンデーションにおける平準化を考慮した2段階最適化⁴

検索エンジンやウェブサービスなどの広告枠では、カスタマーの商品に対するクリック確率など効用を表すスコア順に商品を推薦する方法が一般的です。しかし、この方法では一部の人気商品ばかりが推薦されてしまい、販売を促進したい商品の露出を増やすという広告の本来の目的を達成できないことが少なくありません。そこで、商品毎に事前に定めた目標を満たしつつ（これを「平準化」と呼んでいます）期待利得の合計を最大化する最適化問題を解いて、各広告枠に推薦する商品を決定する方法が考えられます。しかし、カスタマーがウェブサイトを訪問するたびに最適化問題をリアルタイムに解くことは現実的ではなく、開発工数や導入時のリスクを考えると現行の推薦システムを全く新しく作り替えることも容易ではありません。

提案手法では、各商品のスコアを修正する調整係数を求める2段階の最適化問題を事前に解くことで、現行の推薦システムをほとんど変更することなく、平準化を考慮した商品の推薦を実現しました。具体的には、平準化を考慮した広告枠への商品の割当てを求める最適化問題を解いた後に、この最適な割当てを可能な限り再現する各商品のスコアの調整係数を求める最適化問題を解きます。実際には、目標の達成が非常に困難な商品も存在しますので、目標を達成する商品の数を最大化する最適化問題を解いています。この調整係数を推薦システムに事前に渡すことで、カスタマーの訪問時にその場で最適化問題を解かなくても、ほぼ同等の推薦結果が得られるようになりました。

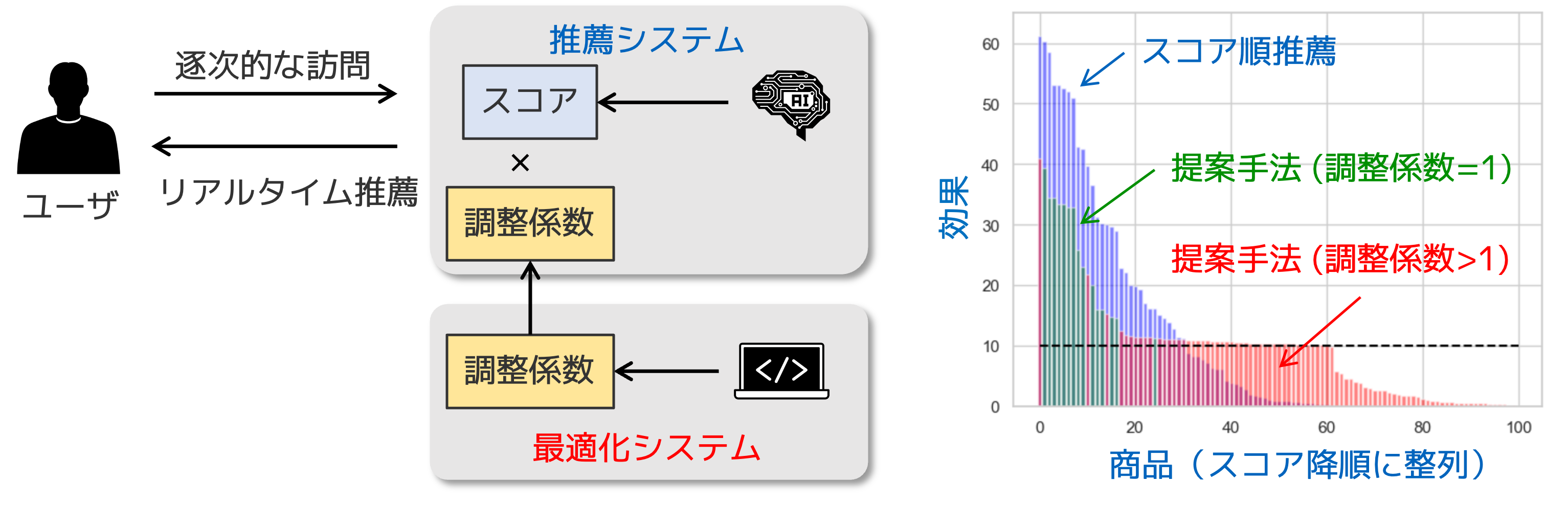
レベニューマネジメントにおける暗黙知を考慮した価格操作範囲の自動設定⁵⁶

ホテルや旅客など在庫を持ち越せない業態のサービスでは、適応的に販売価格を調整するレベニューマネジメントが盛んです。いくつかのサービスでは、現場担当者が経験に従って各商品の販売価格を調整していましたが、商品数の増大にともない作業の支援・自動化が求められるようになりました。そこで、取扱高など与えられたKPIを最大化する最適化問題を解くことで、販売価格の調整にかかる手間を軽減する方法が考えられます。しかし、個々の現場担当者が培ってきた販売価格の調整にかかる暗黙知を数式で表現することは容易ではなく、現場担当者へのインタビューに多くの時間を費やしても最適化問題に定式化することはなお困難です。

提案手法では、過去の作業履歴から個々の現場担当者の暗黙知を抽出し、販売価格の適切な操作範囲の上下限を自動設定するシステムを実現しました。データマイニングでは、支持度の最低値が与えられた下で確信度が最大となる区間を算出する数値属性相関ルールが知られています。しかし、既存手法をそのまま適用すると、販売価格のわずかな違いで操作範囲の上下限が急激に変動する問題が生じます。そこで、価格操作の特性を考慮したモデルにより補正する手法を導入することで、現場担当者の直観に合う販売価格の操作範囲を提示できるようになりました。

数理最適化の活用を促進する基盤技術の開発⁷

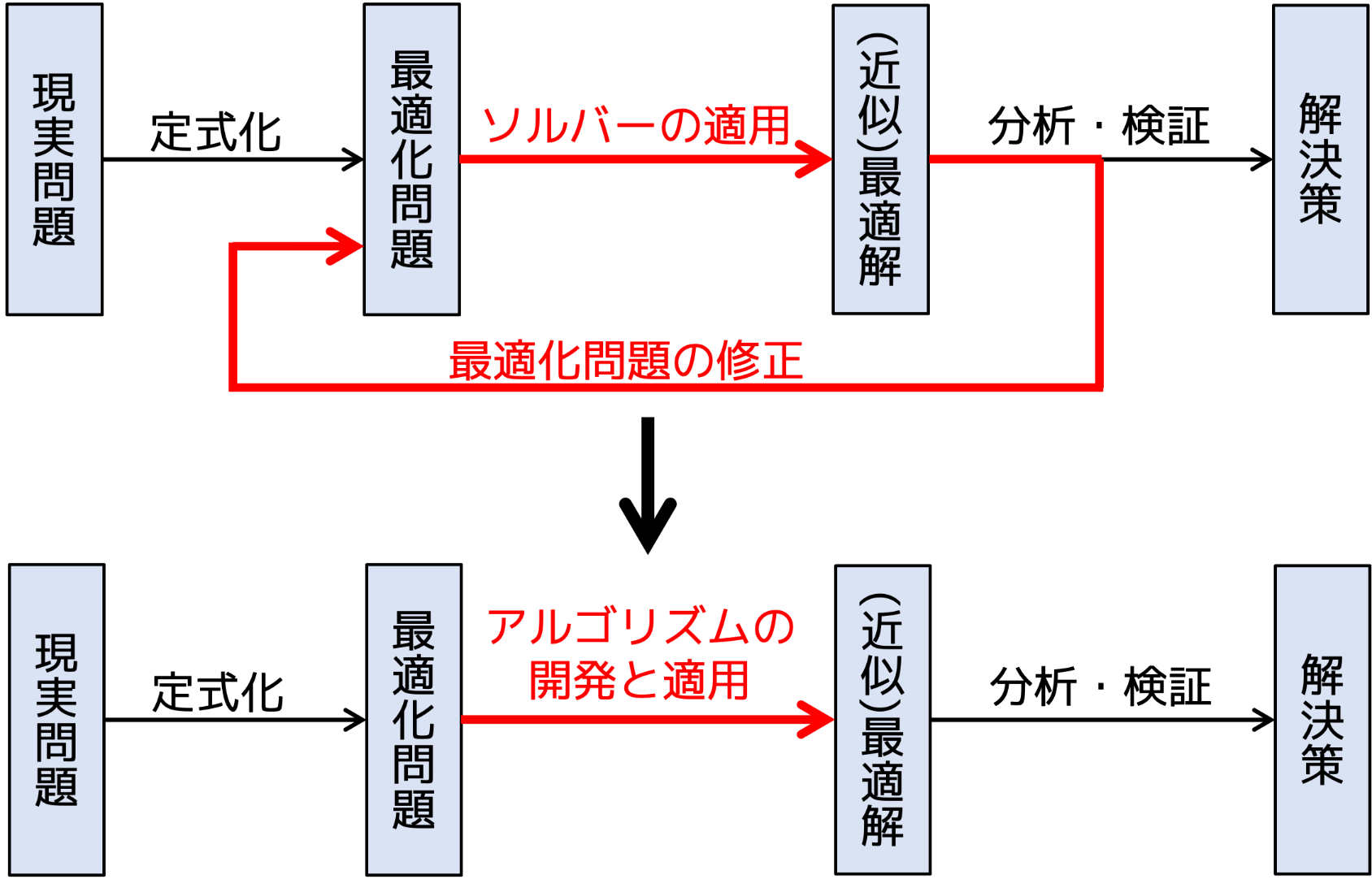
数理最適化を用いた問題解決は、下図に示すように（１）最適化問題の定式化、（２）アルゴリズムによる求解、（３）計算結果の分析・検証、（４）最適化問題の修正という一連の手続きからなります。

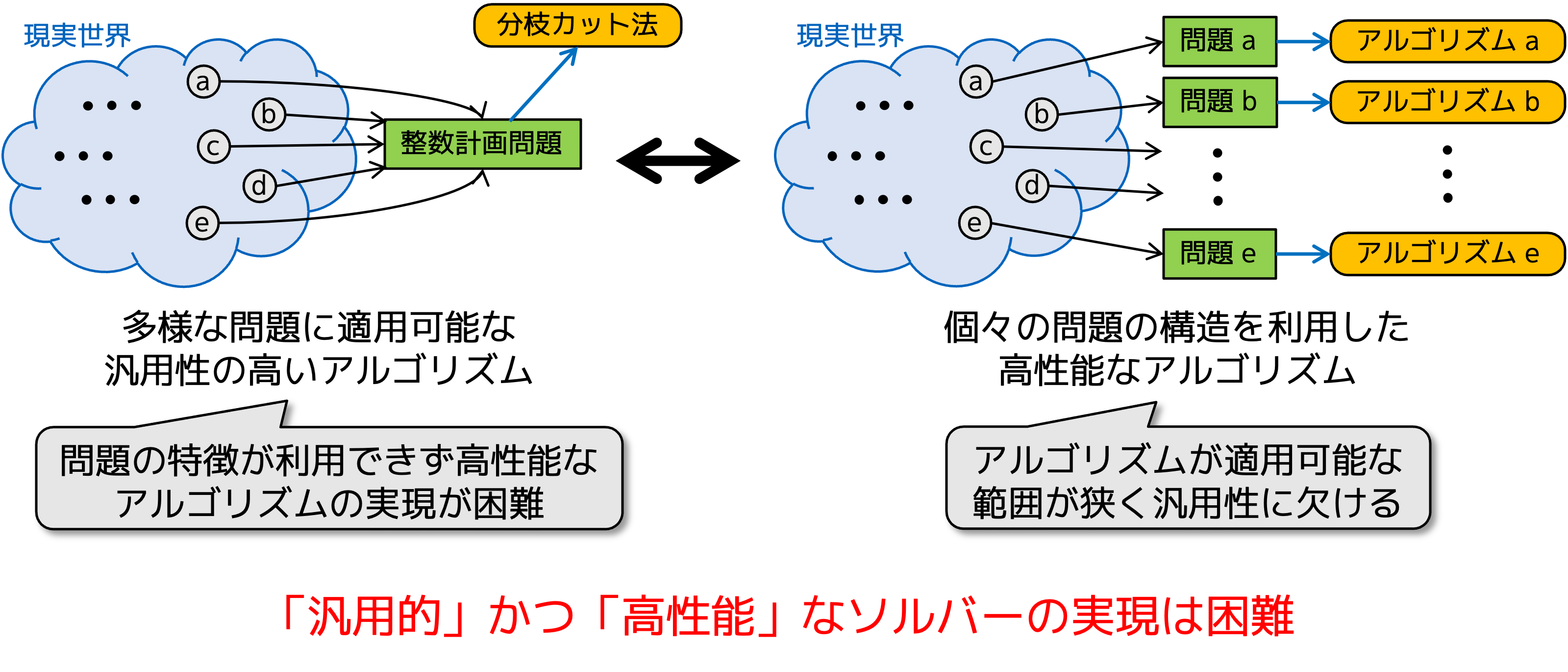
この際にボトルネックとなるのは、最適化問題の修正にともなうアルゴリズムの修正もしくは開発です。要件の変更や追加が生じると、アルゴリズムの大幅な修正もしくは開発が必要となり、数日もしくは数週間、下手をすれば数ヶ月の期間を要する可能性もあります。そのため、下図に示すように、課題の要件と最適化問題の定式化が十分に固まるまでは、できる限り汎用性の高い既存の数理最適化ソルバーを利用して、アルゴリズムの開発を避けることが望ましいです。

整数計画問題は多くの組合せ最適化問題を定式化できる汎用的な最適化問題であり、厳密な最適解を求める分枝カット法にさまざまなアイデアを盛り込んだ高性能な整数計画ソルバーが多く開発されています。しかし、分枝カット法は解候補を体系的に列挙するアルゴリズムで入力データの規模に対して最悪計算時間量が指数関数的に増大するため、計算時間が入力データに敏感になることが少なくありません。また、分枝カット法にもとづく整数計画ソルバーは、あらゆる整数計画問題を効率的に解いてくれるわけではなく、実際には、2次割当問題や配送計画問題など苦手とする組合せ最適化問題が少なくありません。 一方で、現実問題では質の高い近似解で十分に問題解決に役立つ場合が多く、これらの問題では、局所探索法にさまざまなアイデアを盛り込んで探索の集中化と多様化をバランス良く実現するメタヒューリスティクスが多く開発されています。しかし、高性能なメタヒューリスティクスを開発するには個別の問題に含まれる特徴的な構造を利用する必要があるため、専門家であっても新たな問題に取り組むたびにアルゴリズムの開発に多くの時間と手間を要することが少なくありません。このように、高性能かつ汎用的なメタヒューリスティクスを開発することは難しい状況でした。

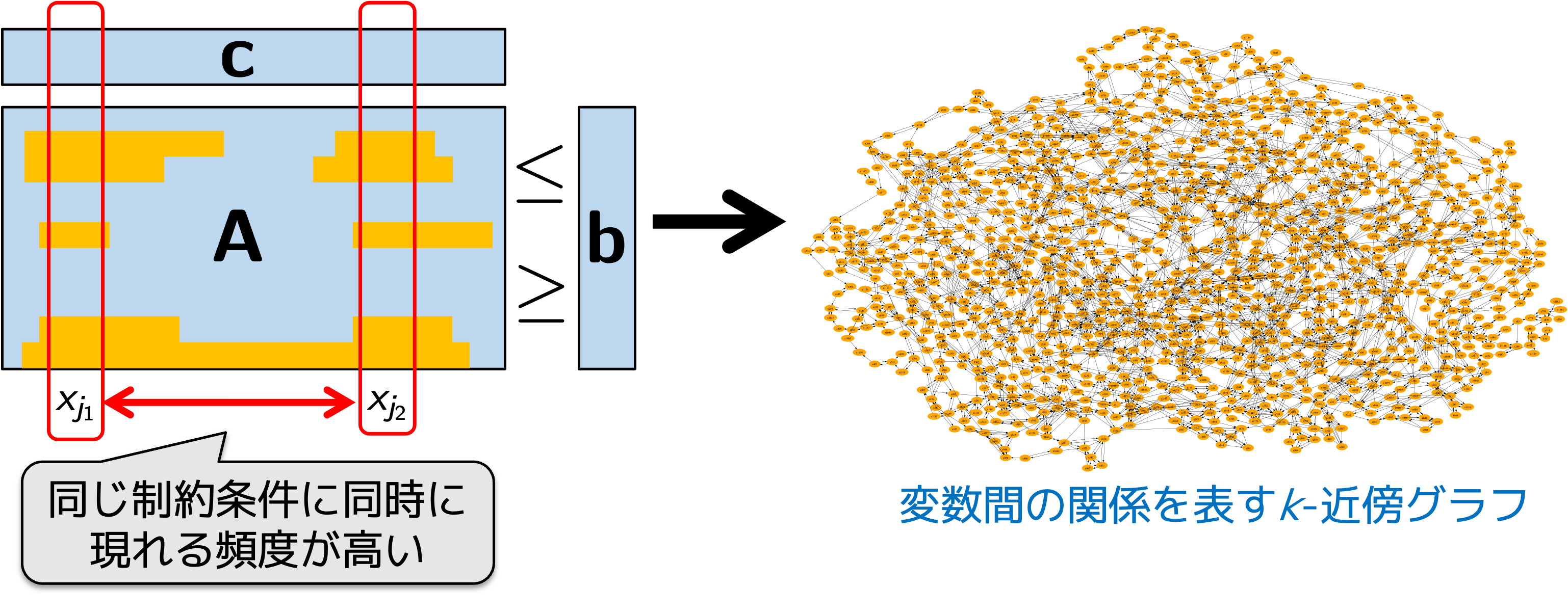
整数計画問題は汎用的な最適化問題であり、その一般形からアルゴリズムの性能向上に役立つ特徴的な構造を見いだすことは困難です。一方で、現実問題を定式化して得られる個別の入力データはネットワーク、論理、順序、割当などの典型的な離散構造で表される特徴的な部分から構成されていることが多いです。また、事前にアルゴリズムの動作仕様を決定する必要はなく、実行時に入力データに合わせてアルゴリズムの一部の動作仕様を変更すれば、個別の入力データから抽出した情報をアルゴリズムの性能向上に利用することは可能です。

このアイデアにもとづいて、大規模な2値整数計画問題に対する効率的なメタヒューリスティクスを提案しました。例えば、2値整数計画問題では、1個の変数の値を反転する操作にもとづく局所探索法が考えられますが、現在の解に与える変化が小さいと、しばしば質の低い近似解（局所最適解）に囚われてしまい十分な性能が得られません。質の低い近似解に囚われることなく広い範囲を探索して質の高い近似解にたどり着くためには、複数の変数の値を同時に反転する近傍操作にもとづく局所探索法を開発する必要があります。提案手法では、データマイニングにおけるk-近傍グラフのアイデアを利用し、同じ制約条件に同時に現れる頻度の高い変数の組を入力データから抽出した上で、近傍内の解候補の探索をこれらの変数の組に制限することで局所探索法の大幅な効率化を実現しました。現在は、これまでに開発したアルゴリズムを多くの人が利用できるように、公開版の実装を進めています。

おわりに

本記事では、リクルートのデータ推進室における数理最適化を活用した問題解決の取り組みを紹介しました。数理最適化を活用した問題解決では2つの事例を紹介しました。また、数理最適化の活用を促進する基盤技術の開発では、大規模な2値整数計画問題に対する効率的なメタヒューリスティクスの開発を紹介しました。 この記事を読んで数理最適化に興味を持たれたら、拙著『しっかり学ぶ数理最適化：モデルからアルゴリズムまで』⁸を手に取っていただけると幸いです。

リクルートでは、人生の節目となる「ライフイベント」領域、日常消費の「ライフスタイル」領域に加えて、近年では、業務・経営支援（クラウドを活用したSaaSソリューション）にも力を入れており、多岐に渡る業界で様々なサービスを提供しています。これらのサービスにおける問題解決に関わる中で、数理最適化の新たな活用事例を開拓する多くの機会に恵まれたことを嬉しく思っています。数理最適化を軸とする新しいサービスを立ち上げて世の中を変える、そういう仕事ができるよう今後も努めたいと思います。

---

1. 梅谷俊治, 組合せ最適化による問題解決の実践的なアプローチ, オペレーションズ・リサーチ 66 (2021), 362-266. ↩︎

2. 西村直樹, 数理最適化技術活用のための取り組みと事例―RECRUIT TECH MEET UP#4― , 2022. ↩︎

3. 須藤遼介, 中村圭太, 濵田賢吾, 棚橋耕太郎, 西村直樹, リクルート事例でわかる数理最適化入門 , 2022. ↩︎

4. 濱田賢吾，西村直樹，梅谷俊治，アイテム推薦における公平性考慮のための二段階最適化，日本オペレーションズ・リサーチ学会春季研究発表会，2023年3月． ↩︎

5. 西村直樹，池田春之介，木村隆介，梅谷俊治，レベニューマネジメントにおける暗黙知を考慮した最適化モデルの自動構成，第23回情報論的学習理論ワークショップ(IBIS2020)，2020年． ↩︎

6. S.Ikeda, N.Nishimura, S.Umetani, Operation range estimation for price optimization, International Workshop on Data Mining for Service (DMS2023), 2023. ↩︎

7. S.Umetani, Exploiting variable associations to configure efficient local search algorithms in large-scale binary integer programs , European Journal of Operational Research, 263 (2017), 72-81. (open access) ↩︎

8. 梅谷俊治, しっかり学ぶ数理最適化：モデルからアルゴリズムまで, 講談社, 2020. ↩︎